|
Lets quickly go over the three questions from the preceding sub-chapter |
|
 |
1. What kind of hystereses curve do I need for the application I have
in mind? |
 |
Lets look at two "paradigmatic" applications: A transformer core and a magnetic memory. |
|
 |
The transformer core is ferromagnetic in order to "transport" a large
magnetic flux B produced by the primary coil to the secondary coil. What I want is that the induced flux B
follows the primary field H as closely as possible. |
|
 |
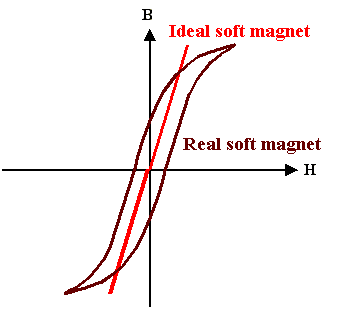
In other words: There should be no hystereses
loop - just a straight line, as shown below |
|
| |
| |
|
 |
The ideal curve, without any hystereses, does not exist. What you get is something
like the curve shown for a real soft magnet - because that is what we call a material with
a kind of slender hystereses curve and thus small values of coercivity and remanence |
 |
If we switch on a positive field H and then go back to zero again, a little
bit of magnetization is left. For a rather small reverse field, the magnetic flux reverses, too - the flux B
follows H rather closely, if not exactly. |
 |
Hystereses losses are small, because
the area enclosed in the hystereses loop is small. |
 |
But some losses remain, and the "transformer core"
industry will be very happy if you can come up with a material that is just 1 % or 2 %
"softer" than what they have now. |
 |
Beside losses, you have another problem: If you vary H sinusoidally, the output
will be a somewhat distorted sinus, because B does not follow H linearly. This may be a problem
when transforming signals. |
|
|
|
 |
A soft magnetic material will obviously not make a good permanent
magnet, because its remaining magnetization (its remanence) after switching off the magnetic field H is small.
|
|
 |
But a permanent magnet is what we want for a magnetic
storage material. Here we want to induce a large permanent magnetization by some external field (produced by the
"writing head" of our storage device) that stays intact for many years if needs be. Some more information about
magnetic storage can be found in an extra module |
|
 |
It should be strong enough - even so it is
contained in a tiny area of the magnetic material on the tape or the storage disc - to produce a measurable effect if the
reading head moves over it. It should not be too strong, however, because that would
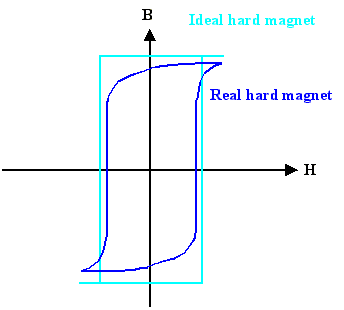
make it too difficult to erase it if we want to overwrite it with something else. In short, it should look like this |
| |
|
|
|
|
 |
We can define what we want in terms of coercivity and remance. Ideally, the hystereses
curve is very "square. |
 |
At some minimum field, the magnetization is rather large and does not change much anymore. |
 |
If we reverse the field direction, not much happens for a while, but as soon as we move above
slightly above the coercivity value, the magnetization switches direction completely. |
 |
Ferromagnetic losses are unavoidable, we simply must live with them |
| |
|
 |
Pretty much all possible applications - consult the list in the next section -
either calls for soft or for hard magnets; there
isn't much in between. |
|
 |
So we now must turn to the second and third
question: |
| |
|
|
Tailoring Hystereses Curves |
| |
|
 |
The question was: What is available
in terms of hystereses curves? Good question; it immedately provokes another questions: |
|
 |
What is available in terms of ferromagnetic materials?
The kind of hystereses behavior you get is first of all a property of the specific material you are looking at. |
|
 |
For arbitrary chemical compounds, there is little predictive power if they are
ferromagnetic or not. In fact, the rather safe bet is that some compound not containing
Fe, Ni, or Co is not ferromagnetic. |
|
 |
Even if we restrict ourselves to some compound or alloy containing at least one
of the ferromagnetic elements Fe, Ni or Co, it is hard to predict if the result will be ferromagnetic
and even harder to predict the kind of hystereses curve it will have. Pure Fe in its (high temperature) fcc
lattice variant is not magnetic, neither are most variants of stainless steel, for example. |
 |
But progress has been made - triggered by an increasing theoretical understanding
(there are theories, after all), lots of experience and semi-theoretical guide lines - and just plain old trying out in
the lab. |
|
 |
This is best demonstrated by looking at the "strength"
of permanent magnets as it went up over the years: |
|
|
 |
Not bad. And pretty exotic materials emerged. Who thinks of Cobalt - Samarium
compounds, or Neodymium - iron - boron? |
|
 |
What will the future bring. Well, I don't know and you shall see! |
|
 |
But we can do a little exercise to get some idea of what might be possible |
| |
|
 |
The final question was: Can I change the hystereses curve of a given material
in a defined direction? |
|
 |
The answer is: Yes, you can - within limits, of course. |
|
 |
The hystereses curve results from the relative ease or difficulty
of moving domain walls in a given material. And since domain walls interact with
stress and strain in a material, their movement depends on the internal structure of the material; on the kind and density
of crystal lattice defects. |
 |
This is best illustrated by looking at hystereses curves of one
and the same material with different internal structures. |
| | |
|
|
|  |
There is a big difference for annealed, i.e. relatively defect
free iron and heavily deformed iron, i.e. iron full of dislocations, as the figure on the left nicely illustrates |
 |
We will find similar behavior for most ferromagnetic materials (not for all, however, because
some are amorphous). |
 |
Instead of manipulating the defects in the materials to see what kind of effect we get, we
can simply put it under mechanical stress, e.g. by pulling at it. This also may change the hystereses curve very much: |
| |
| | |
 |
Here we have the hystereses curves of pure Ni samples with and without
mechanical tension. The effects are quite remarkable |
|
|
| |
|
|
 |
In this case the tension force was parallel to the external field
H |
 |
In this case the tension force was at right angles to
the external field H |
|
 |
There is a big change in the remanence, but not so much difference in the coercivity. |
 |
Big changes in the remanence, not so much effect in the coercivity. We have an almost box-like
shape, coming close to the ideal hard magnet from above. |
 |
The final word thus is: |
|
 |
There is a plethora of ways to design ferromagnetic properties out there. The trouble
is, we are just learning now how to do it a little bit better than by pure trial and error. |
|
 |
The future of magnetism looks bright. With an increased level of understanding,
new materials with better properties will result for almost sure. Time will tell. |
© H. Föll (Electronic Materials - Script)