|
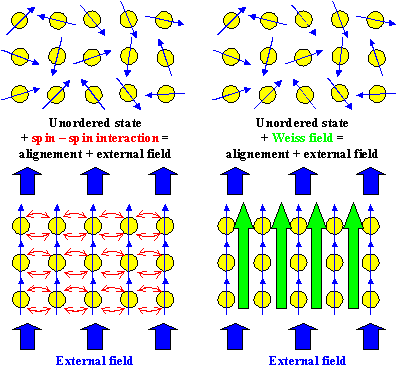
In ferromagnetic materials the magnetic moments of the atoms are "correlated"
or lined-up, i.e. they are all pointing in the same direction | |
|
|
 |
The physical reason for this is a quantum-mechanical spin-spin interaction that
has no simple classical analogue. | |
|
 |
However, exactly the same result - complete line-up - could be obtained, if the magnetic moments
would feel a strong magnetic field. | |
|
 |
In the "mean field" approach or the "Weiss" approach to ferromagnetism,
we simply assume such a magnetic field HWeiss to be the cause for the line-up of the magnetic moments.
This allows to treat ferromagnetism as a "special" case of paramagnetism, or more generally, "orientation
polarization". | |
| | |
| |
 |
For the magnetization we obtain Þ |
|
| J | = |
N · m · µ0 · L(b) |
= |
N · m · µ0 · L |
æ
è |
m · µ0 · (H + w · J)
kT | ö
ø
|
|
|
|
 |
The term w · J describes the Weiss field via Hloc
= Hext + w · J; the Weiss factor w is the decisive (and unknown)
parameter of this approach. | |
|
 |
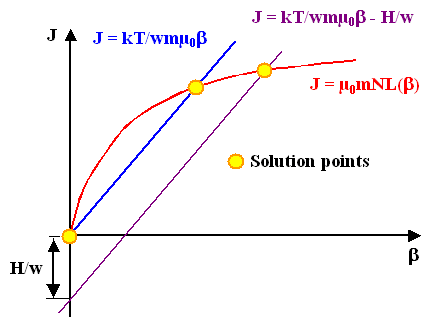
Unfortunately the resulting equation for J, the quantity we are after, cannot
be analytically solved, i.e. written down in a closed way. | |
| | |
| |
 |
Graphical solutions are easy, however Þ |
|
|
|
 |
From this, and with the usual approximation for the Langevin function for small arguments,
we get all the major ferromagnetic properties, e.g. - Saturation field strength.
- Curie temperature TC.
| TC | = |
N · m
2 · µ02 · w
3k |
|
- Paramagnetic behavior above the Curie temperature.
- Strength of spin-spin interaction via determining w from TC.
| |
|
 |
As it turns out, the Weiss field would have to be far stronger than what is technically achievable
- in other words, the spin-spin interaction can be exceedingly strong! | |
| | |
| |
 |
In single crystals it must be expected that the alignments of the magnetic moments
of the atom has some preferred crystallographic direction, the "easy" direction. |
|
Easy directions:
Fe (bcc) <100>
Ni (fcc) <111>
Co (hcp) <001> (c-direction) |
|
| | |
| |
 |
A single crystal of a ferromagnetic material with all magnetic moments aligned
in its easy direction would carry a high energy because: | |
|
|
 |
It would have a large external magnetic field, carrying field energy. |
|
 |
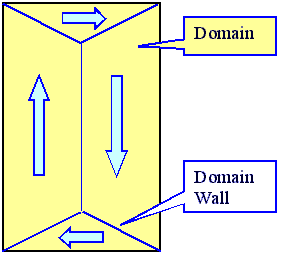
In order to reduce this field energy (and other energy terms not important here),
magnetic domains are formed Þ. But the energy gained has to be "payed for"
by: | |
|
 |
Energy of the domain walls = planar "defects" in the magnetization structure. It
follows: Many small domains —> optimal field reduction —> large domain wall energy "price". |
|
|
 |
In polycrystals the easy direction changes from grain to grain, the domain structure has to
account for this. | |
|
 |
In all ferromagnetic materials the effect of magnetostriction (elastic deformation tied to
direction of magnetization) induces elastic energy, which has to be minimized by producing a optimal domain structure. |
|
 |
The domain structures observed thus follows simple principles but can be fantastically
complicated in reality Þ. | |
| |
| |
 |
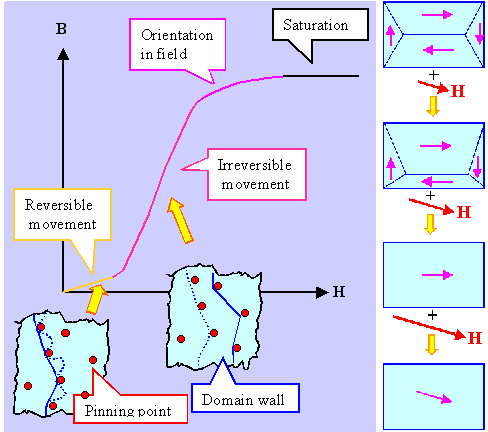
For ferromagnetic materials in an external magnetic field, energy can be gained
by increasing the total volume of domains with magnetization as parallel as possible to the external field - at the expense
of unfavorably oriented domains. | |
|
|
 |
Domain walls must move for this, but domain wall movement is hindered by defects because of
the elastic interaction of magnetostriction with the strain field of defects. |
|
|
 |
Magnetization curves and hystereses curves result Þ,
the shape of which can be tailored by "defect engineering". |
|
 |
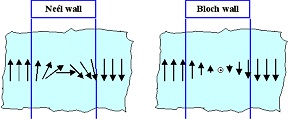
Domain walls (mostly) come in two varieties:
- Bloch walls, usually found in bulk materials.
- Neél walls, usually found in thin films.
| |
|
|
| |
|
| |
| |
 |
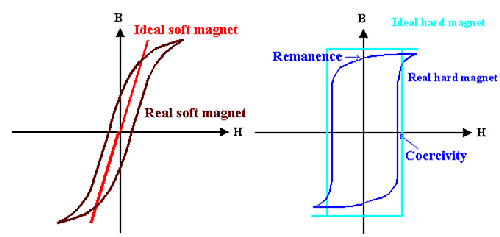
Depending on the shape of the hystereses curve (and described by the values of
the remanence MR and the coercivity HC, we distinguish hard and soft magnets
Þ. | |
|
 |
Tailoring the properties of the hystereses curve is important because magnetic
losses and the frequency behavior is also tied to the hystereses and the mechanisms behind it. |
|
|
 |
Magnetic losses contain the (trivial) eddy current losses (proportional to the conductivity
and the square of the frequency) and the (not-so-trivial) losses proportional to the area contained in the hystereses loop
times the frequency. | |
|
 |
The latter loss mechanism simply occurs because it needs work to move domain walls. |
|
 |
It also needs time to move domain walls, the frequency response of ferromagnetic
materials is therefore always rather bad - most materials will not respond anymore at frequencies far below GHz. |
|
| |
|
|
© H. Föll (Electronic Materials - Script)