|
Pure metals are rarely used - in the real world you use alloys. |
|
 |
In principle, the specific resistivity r
of an alloy can be obtained from the phase diagram
and the r - values of the phases involved. Lets look at the extremes: |
 |
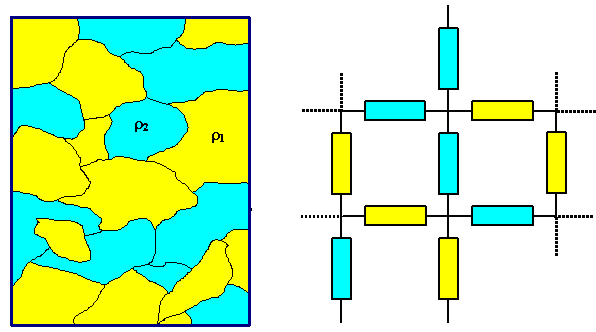
1. Complete immiscibility,
e.g. in the case of Au/Si, or Cu/W. We may treat the resulting mix of metal particles as a network
of resistors being linked in series and parallel. The volume fractions of the phases would constitute the weights
- the treatment is not unlike the elastic modulus of
compounds. |
| |
|
|
 |
But no matter what kind of volume fraction you use and how you treat the resistor network
- the resulting resistivity will never be smaller than that of the ingredient with the
smallest resistivity. |
 |
2. Complete miscibility (e.g. Au/Ag,
Cu/Ni). Experimentally we find for small amounts (some %) of B in A (with [B] = concentration
of B) |
| |
|
|
 |
This formula is a special case of Nordheims
rule which states . |
|
|
|
r » XA · rA
+ XB · rB + const. · XA
·XB |
|
|
|
 |
This is pretty much an empirical law, it does not pay to justify it theoretically. Again,
it is not possible to produce an alloy with a resistivity smaller than one of its components. |
 |
If you have intermetallic compounds in your
phase diagram, use Nordheim's rule with the intermetallic phases as XA and XB. |
|
 |
This leaves open the possibility that some intermetallic phase, i.e. a defined compound with its own crystal
lattice, might have a lower resistivity than its constituents. While this is unlikely (if not outright impossible?) on theoretical
grounds, no such intermetallics have been found so far. |
 |
The sad fact then is that unleashing the full power of metallurgy and chemistry on mixing conductors
(i.e. metals), will not give you a conductor with a specific conductivity better than Ag. |
|  |
You will have to turn to superconductors (forgetting about cost considerations),
if you can't live with Ag. |
© H. Föll (Electronic Materials - Script)