7.1.4 Der E - Modul von Verbundwerkstoffen

Was ist ein Verbundwerkstoff?

Bisher haben wir implizit immer die mechanischen Eigenschaften homogener Körper betrachtet. Das ist nicht besonders realistisch. Sowohl in der Technik als auch in der Natur finden wir oft inhomogene Materialien. Viele davon sind gezielt erzeugte Verbundwerkstoffe.
Bevor wir uns der allgemeinen Beschreibung von Spannungs- und Dehnungszuständen widmen, wollen wir deshalb erst noch schnell sehen, wie man die elastischen Eigenschaften eines Verbundwerkstoffs aus den elastischen Eigenschaften seiner Konstituenten bestimmt.
Verbundwerkstoffe (engl. compounds) nennen wir alle Materialien, die aus mindestens zwei verschiedenen Phasen oder Komponenten bestehen. Es gibt natürliche und künstliche Verbundwerkstoffe; zum Beispiel:
Natürliche Verbundwerkstoffe:
  • Holz - Lange Zellulosefasern in einer Matrix aus Zellulose/Lignin (es lohnt sich, den "Holzartikel" im "Ashby und Jones" zu lesen
  • Granit - ein Gemisch aus Feldspat, Quarz und meist dunkler Minerale wie Glimmer, Hornblende, Pyroxen.
  • Wirbeltiere - ein Verbund aus harten Knochen und weichem Gewebe.
Künstliche Verbundwerkstoffe:
  • Damaszenerstahl - ein Gemisch von weichem und harten Eisen (Stahl), von den Kelten schon ca. 500 v.Ch. erfunden (nicht in Damaskus!).
  • Reflexbogen; engl. "compound bow" (= Verbundbogen), ein Bogen aus verschiedenen Holzsorten und Horn; dem einfachen Holzbogen überlegen.
  • Beton (gab es schon bei den Römern; die Kuppel des Pantheon, immer noch eine der größten Kuppeln der Welt ist aus einer Art Beton). Beton ist ein Gemisch aus größeren harten Kieselsteinen in einer Zementmatrix, die deutlich andere mechanische Eigenschaften hat als die Steine.
  • Stahlbeton - d.h. Stahlstäbe oder -geflecht eingebettet in Beton.
  • "GFK" und "CFK", d.h. Glasfaser oder Carbonfaser eingebettet in Kunststoff. Das Airbus Leitwerk ist das prominenteste Beispiel des high-tech Einsatzes von CFK Materialien.
  • Ein Kristall mit Ausscheidungen einer anderen Phase - d.h. so gut wie jede Legierung.
Verbundwerkstoffe, in dieser breiten Definition, sind die reale Welt. Was sind die mechanischen Eigenschaften eines Verbundwerkstoffs? Können wir sie aus den mechanischen Eigenschaften der Komponenten ableiten?
Wenn man die Fülle an verschiedenartigen Beispielen anschaut, scheint dies ein hoffnungsloses Unterfangen zu sein. Dem ist aber nicht so, falls wir uns auf elastisches Verhalten beschränken - plastisches Verhalten oder Bruch ist in der Tat nicht ganz einfach darstellbar.
Wir können mit jedem Verbundwerkstoff einen Zugversuch machen. Das Ergebnis wird jetzt möglicherweise davon abhängen, in welche Richtung wir ziehen - z.B. parallel oder senkrecht zu den Fasern eines GFK Materials. Wir können aber in jedem Fall den elastischen Bereich definieren (Verformung vollständig reversibel) und einen E-Modul EV = ds/de sowie eine Querkontraktionszahl nV des Verbundmaterials angeben; oder alternativ Kompressionsmodul und Schermodul.
Die gute Nachricht dazu ist, daß EV in einfachster Weise von den E-Moduls der beteiligten Materialien abhängt - es ist völlig analog zur Reihen- und Parallelschaltung von Widerständen.
 
Der E-Modul eines idealisierten Faserverbundwerkstoffs
   
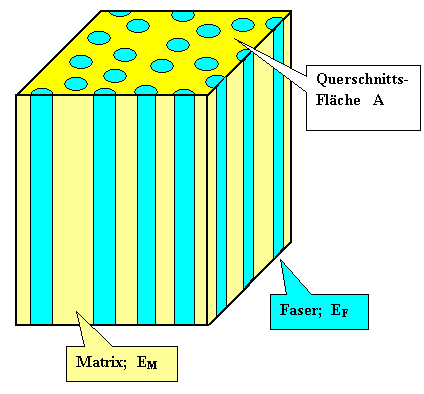
Betrachten wir zunächst einen idealisierten Verbundwerkstoff: Harte Fasern (d.h. großer E-Modul) in einer weichen (kleiner E-Modul) Matrix. Die Fasern sollen alle parallel und gerade durch die Matrix laufen.
Das sieht dann so aus:
Faser Verbundwerkstoff
Die Fasern haben einen E-Modul EF, die Matrix hat EM; es ist EF > EM.
In der Aufsicht haben die Fasern eine gesamte Querschnittsfläche AF relativ zur betrachteten Gesamtfläche A.
In unserer einfachen Geometrie ist damit VF, der Volumenanteil der Fasern, gegeben durch VF = AF/A.
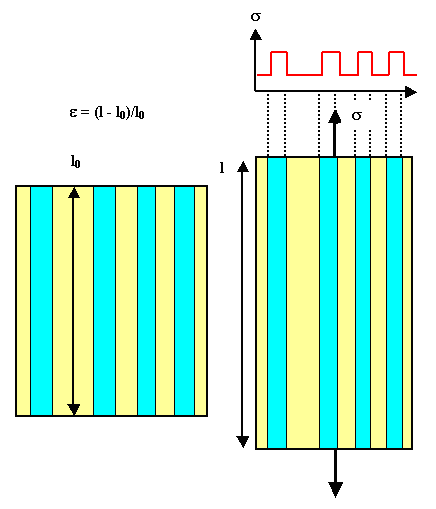
Wir machen jetzt zwei Zugversuche: Einmal parallel, und einmal senkrecht zu den Fasern. Dabei setzen wir nur voraus, daß die Haftung der Fasern in der Matrix so gut ist, daß der Verbundwerkstoff zusammenhält, d.h. daß wir nicht zum Beispiel nur die Fasern aus der Matrix ziehen.
Wir betrachten beide Versuche parallel
Zugversuch parallel zur Faser Zugversuch senkrecht zur Faser
Bedingung: Die Dehnung e ist auf jeder Querschnittsfläche gleich groß Bedingung: Die Spannung s ist auf jeder Querschnittsfläche gleich groß. Falls das schwer einzusehen ist: Die "Schneideprozedur" anwenden
 
Verbundmaterial; Dehnung parallel Fasern
Verbundwerkstoff; Zug senkrecht Faser
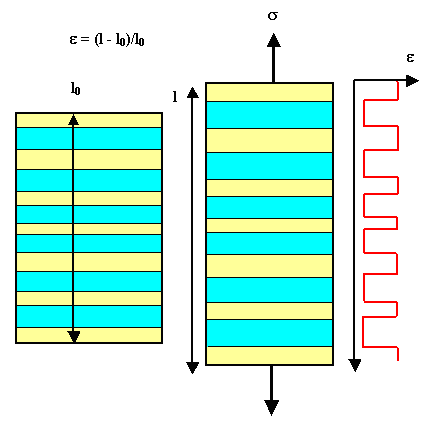
Die Spannung muß auf der Querschnittsfläche variieren - um die Fasern um e zu dehnen muß man auf der Faserquerschnittsfläche mehr Kraft anwenden als auf einer gleichgroßen Fläche der Matrix Die Dehnung variiert. Die Fasern werden weniger stark gedehnt als die Matrix
In Formeln haben wir In Formeln haben wir
e   =  eF  =   eM
   
sF   =  EF · e
   
sM   =  Em · e
e = VF · eF + VM · eM
 
da sich die gesamte Dehnung als Summe der Dehnung in den relativen Volumenanteilen von Faser und Matrix darstellt.
Wir machen jetzt einen kleinen Umweg und berechnen die Kraft F, die auf die gesamte Querschnittsfläche wirken muß Mit VM  =  1 – VF ergibt sich
F  =   sF · AF + sM · (A – AF)
 
e  =  VF · eF + (1 – VF) · eM
Die auf die Querschnittsfläche wirkende effektive Spannung sVB ist dann einfach F/A, oder
 Die Dehnungen lassen sich über den E-Modul als Spannungen ausdrücken, wir haben
sVB =   sF · AF
A 		   +  sM · A – AF
A 
 
e  =   VF · s
EF		  +  (1 – VF ) · s
EM
Mit den Beziehungen sF,M = e · EF,M, und AF/A = VF, erhalten wir oder
sVB =  e · æ
è 		EF · VF  +  EM · (1 –  VF ö
ø
 
e  =  s · æ
è 		VF
EF		   +  1 – VF
EM		 ö
ø
 
Der Ausdruck in der Klammer ist natürlich nichts anderes als der effektive E-Modul Epa des Verbundwerkstoffs parallel zur Faser. Wir haben also als Endergebnis Der Ausdruck in der Klammer ist natürlich nichts anderes als der reziproke effektive E-Modul Ese des Verbundwerkstoffs senkrecht zur Faser. Wir haben also als Endergebnis
Epa = EF · VF + EM · (1 – VF)
 
Ese =



1
 VF
EF		 + 1 – VF
EM
Wir haben also für die beiden Extremfälle den effektiven E-Modul des Verbundwerkstoffes, d.h. den E-Modul, der sich experimentell aus einem Zugversuch ergibt, als Funktion der drei Grundvariablen E-Module der Komponenten und Volumenanteil einer Komponente ausgerechnet.
Wie schon angekündigt, sind die Formeln identisch zu den Formeln für Gesamtwiderstände bei Reihen- und Parallelschaltung. Das ist natürlich kein Zufall, sondern unvermeidlich, denn das Ohmsche Gesetz U = R · I und das Hookesche Gesetz s = E · e sind nicht nur mathematisch identisch sondern auch physikalisch sehr ähnlich: Eine "treibende Kraft"; eine allgemeine Ursache, bewirkt in linearer Weise eine "Antwort".
 
Verallgemeinerung
   
Reale Verbundwerkstoffe sind nicht so ideal ordentlich wie unsere obige Modellsubstanz. Beispielsweise kann folgendes passieren:
Die Fasern laufen nicht gerade durch die Matrix, sondern gekurvt. Sie sind nicht beliebig lang, sondern haben irgendeine Längenverteilung. Es sind gar keine Fasern, sondern irgendwelche dreidimensionalen Körper, z.B. Kieselsteine im Zement.
Was bekommen wir dann?
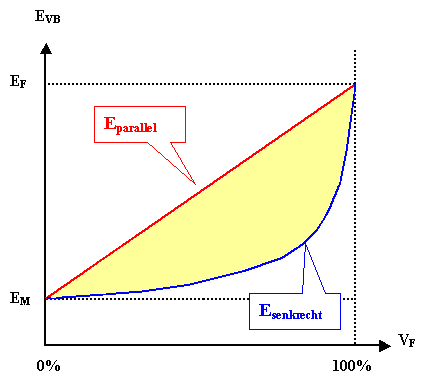
Schauen wir uns dazu die beiden obigen Formeln in einer (schematischen) graphischen Darstellung an:
E-Modul Bereich von Verbundwerkstoffen
Jetzt stellen wir uns Variationen der berechneten Strukturen vor, z.B. Fasern die unter irgendeinem Winkel zur Zugrichtung verlaufen, also weder parallel noch senkrecht.
Der Verlauf von EVB muß dann irgendwo zwischen der roten und der blauen Kurve liegen, denn diese geben die jeweiligen Extremwerte - den größt- und kleinstmöglichen Modul - für eine gegebene Zusammensetzung
Und das gilt für jede denkbare Konfiguration von Matrix und "Fasern". Der E-Modul liegt für eine gegebene Zusammensetzung im gelben Feld.
Wo genau - das wissen wir nicht. Dazu müßte man für die gegebene Struktur Rechnungen anstellen, die in der Regel nicht ganz einfach sind.
Trotzdem sind unsere simplen Formeln bemerkenswert. Sie sagen uns nicht nur was überhaupt möglich ist, sondern auch wie man optimiert; d.h. ob Variationen von Formen und Strukturen den E-Modul in Richtung größer oder kleiner ändern werden.
Mit Frame Zurueck Weiter als PDF

© H. Föll (MaWi 1 Skript)