|
|
 |
Schon die reine Dreh-KWKG auf {111} ist viel
komplizierter: |
|
 |
Abbildung: Die <111> Kleinwinkel-Drehkorngrenze in
Silizium |
|
|
 |
 |
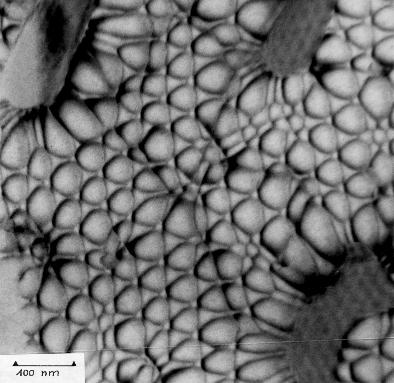
Das ist die im Kapitel 1 gezeigte Folie zur Illustration der
Komplexität der Natur. Jetzt kann das Bild verstanden werden. 4 Schritte
sind erforderlich: |
|
 |
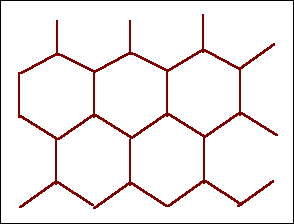
1. Das Netzwerk wird dreizählige Symmetrie haben müssen, d.h. wir
brauchen einen Satz von 3 Schraubenversetzungen
 |
|
 |
2. Die 6-er Knoten sind nicht stabil, das Netzwerk spaltet auf in die
stabile Konfiguration (andere Skala!)
 |
|
 |
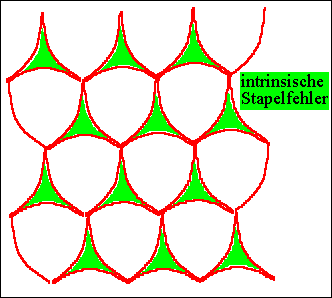
3. Die Versetzungen sind aufgespalten, jeder 2. Knoten kann Energie
gewinnen durch möglichst große Abstände zwischen den
Partialversetzungen mit nur wenig zusätzlicher Stapelfehlerfläche
 |
|
 |
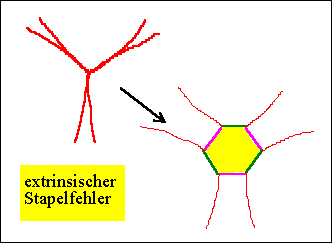
4. Die noch hochenergetischen "eingeschnürten" Knoten finden
ebenfalls eine Möglichkeit, unter Energiegewinn aufzuspalten, dabei wird
ein extrinsischer Stapelfehler gebildet; alle Versetzungen sind Shockleysche
Teilversetzungen
 |
|
 |
5. Das komplette Netzwerk sieht aus wie nebenstehend gezeigt; es entspricht
exakt dem TEM-Bild. Die Größe der aufgespaltenen Knoten hängt
natürlich von der Stapelfehler-Energie ab; hier können sich kubische
Kristalle noch kräftig unterscheiden.
 |
 |
Verallgemeinerungen |
|
 |
1. Franksche Formel. Der (indirekte) Zusammenhang zwischen dem
Abstand von Versetzungen mit Burgersvektor b (der beliebig sein kann),
dem Drehwinkel a (der im Prinzip auch beliebig sein kann) und der Ebene, in dem
die KG liegt, ist wie folgt: |
|
|
 |
|
 |
2. Beliebige KWKG (Also Mischungen aus reiner Kipp- und reiner
Dreh-KWKG). Ist in der verallgemeinerten Frankschen Formel enthalten,
allerdings sagt die Formel nichts über die Geometrie des Netzwerks. Dazu
muß die (komplizierte) Bollmannsche O-Lattice Theorie herangezogen
werden. |
|
 |
3. Große Winkel; also beliebige Korngrenzen. Die Franksche
Formel führt dann auf Abstände zwischen Versetzungen mit
"normalen" Burgersvektoren (vollständiege oder
Partialversetzungen), die im Bereich der Gitterkonstante liegen, also sinnlos
sind. Ausweg: |
|
 |
4. Korngrenzen mit Netzwerken aus KG-Versetzungen, also mit
Burgersvektoren aus dem DSC-Gitter der nächstgelegenen low-
S Orientierung. Die beliebige KG wird demnach
aufgefaßt als eine KG in einer exakten low- S
Orientierung plus eine überlagerte KWKG im zugehörigen DSC-Gitter.
Die Franksche Formel kann weiterhin angewendet werden. Die Geometrien
können extrem kompliziert werden, da allerlei Perversitäten
dazukommen können (z.B. die Aufspaltung von Versetzungen im DSC-Gitter in
Partialversetzungen im DSC-Gitter unter Bildung von Stapelfehlern im DSC-Gitter
(in Silizium beobachtet)). |
|
 |
5. Korngrenzenversetzungen (auch sekundäre Versetzungen genannt
in Abgrenzung zu den primären Versetzungen des "perfekten"
Kristalls) sind i.a. mit Stufen in der Ebene der KG verbunden.
Ein Beispiel zeigt: |
|
|
Abbildung: Sekundäre Versetzung (b=a/10[130]) in einer
S=5 Korngrenze.
- Es ist eine Stufe entstanden; die Stufenhöhe ist ebenfalls im
DSC-Gitter definiert.
- Die Beziehung zwischen Stufe und Versetzung ist nicht trivial.
|
|
 |
6. Korn- und Phasengrenzen können außer
sekundären Versetzungen auch reine Stufen ohne
Versetzungscharakter enthalten. |
|
|
Der Unterschied liegt im Spannungsfeld.
- Versetzungen haben Spannungsfelder, die mit |b| /r abklingen
und weitreichend sind,
- reine Stufen haben kein weitreichendes Spannungsfeld
|
 |
Eine nähere Betrachtung erfolgt im
Kapitel 8: Phasengrenzen |






