7.2.4 Generalization

	The relation between the spacing of the dislocations and the tilt- or twist angle in the special cases given was simple enough - but what about arbitrary small angle grain boundaries with twist and tilt components? What kind of dislocation structure and what geometry should be expected?
		As we have seen, the detailed structure of the network can be quite complicated and depends on materials parameters like stacking fault energies. We can not expect to have a simple formula giving us the answers.
		The relation between the distance between dislocations in a boundary and the orientation relationship for arbitrary low-angle orientations (meaning that the two rotation angles needed for a general description are both small, lets say <=10o - 15o) was first given by Frank. It is Franks formula referred to before.
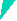	Franks formula is derived in the advanced section, here we only give the result. The low-angle grain boundary shall be described by:
		Its dislocation network consisting of dislocations with Burgers vectors b.
		An arbitrary vector r contained in the plane of the boundary.
		A (small) angle a around an arbitrary axis described by the (unit) vector l (then one angle is enough) that describes the orientation relation ship between the grains. We may then represent the rotation by a polar vector a=a·l
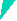	Franks formula then writes:
		d=(r x l)·2sina/2
		with d=sum of all the specific Burgers vectors bi cut by r: d=Sbi; and summing over all i´s.
		Since the formula is formally applicable to any boundary but does not make much sense for large angles a (can you see why?) we only consider low-angle boundaries. Then we can replace sina/2 approximately by a/2 and obtain the simplified version
		d=(r x l)·a
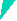	This "simple" formula contains the special cases that we have considered before, and leaves enough room for complications. It does not, however, say anything about preferred planes or network geometries. For this one needs the full power of Bollmanns O-lattice theory.

	Franks formula is not applicable to large angle grain boundaries because the distance between the dislocations would become so small as to be meaningless.
		In this case the grain boundary may be viewed as the (dislocation free) "low S" boundary closest to the actual orientation with a superimposed low-angle grain boundary formed by dislocations in the corresponding DSC lattice.
		Franks formula can then be used for the low angle part and will give the correct over-all Burgers vector count.
	The precise geometry of the network, however, can become hopelessly complicated because all the additional features, e.g., extrinsic dislocations and steps, are not only still present but become more complicated, too. In addition, some special perversities may evolve, e.g. the splitting of DSC lattice dislocations into partial dislocations in the DSC lattice producing stacking faults in the DSC lattice!
		And we are implicitly talking grain boundaries between cubic crystals! In less symmetric crystals everything is even more complicated - it is time then to study O-lattice theory!
	One last feature should be mentioned that now can be understood: The reactions of lattice dislocation that move into grain boundaries. So far, a grain boundary was just seen as an internal surface on which a dislocation can somehow end.
		Now we know better: It simply decomposes into the intrinsic (DSC-lattice) grain boundary dislocations present. This is quite satisfying because the logical problems encountered when thinking more in more detail about how a dislocation "just ends" on a grain boundary. It is also what one sees if looking closely, an example is shown in the illustration.