|
|
 |
Zufällig entstandene
Kleinwinkelkippkorngrenze in Silizium |
|
 |
Schematische Darstellung der Struktur |
|
|
 |
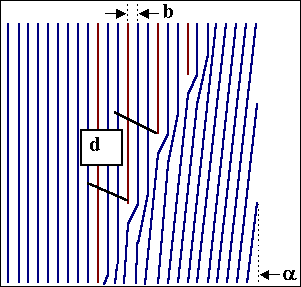Der Abstand d der Versetzungen ist mit dem Kippwinkel
a durch die Beziehung
a=|b|
/d für kleine a
gegeben. Dies ist eine simple Version der
Frankschen Formel zur Beziehung von
Versetzungsgeometrie und Orientierung von Korngrenzen. |
|
|
|
|
|
Abbildung: TEM-Aufnahme einer
Kleinwinkel-Kippkorngrenze |
|
|
|
|
Die <100> Kleinwinkel-Drehkorngrenze in
Silizium |
|
|
Herstellung: Zwei leicht verdrehte Silizium-Proben mit {100}
Oberflächen "verschweißen" bzw. zusammensintern
("Waferbonding"). |
|
Abbildung: TEM-Aufnahme der entstandenen
Kleinwinkel-Drehkorngrenze |
|
|
 |
|
|
Sichtbar ist ein quadratisches Netzwerk von
Schraubenversetzungen (Kontrastanalyse!) und einige "Störungen".
|
|
Analyse der Auswirkungen des
Schraubenversetzungsnetzwerks |
|
|
{100}-Netzebenen oberhalb und unterhalb der Korngrenze für
Drehwinkel=0 (trivial).
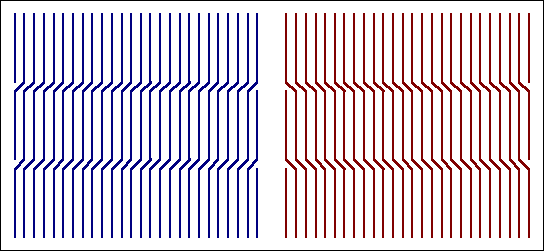Die Einführung zweier Schraubenversetzungen führt zu verschiedenen
Verbiegungen der Netzebene; hier für unter- (links) und oberhalb (rechts)
der Korngrenze gezeichnet. Die gesamte Wirkung zeigt das nächste Bild:
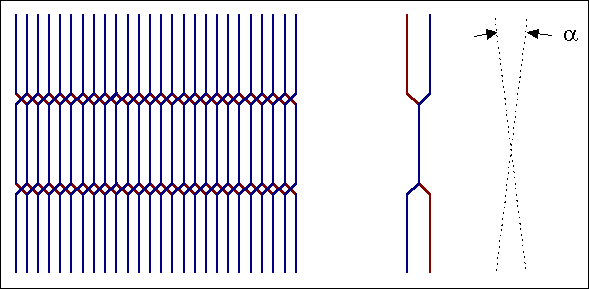 Eine Drehung
der Netzebenenschar um a ist die Konsequenz.
|
|
Will man nicht nur eine Netzebenenschar drehen, sondern den
ganzen "oberen" Kristall, braucht man mindesten einen zweiten Satz
von Schraubenversetzungen. Damit entsteht ein Versetzungsnetzwerk, das
in seiner exakten Struktur - bei immer gleichem Drehwinkel a - von vielen Parametern abhängt, nämlich: |
|
|
Dem Drehwinkel a |
|
|
Den Burgersvektoren der beteiligten Versetzungen
(perfekt, partiell, Korngrenzen-Versetzungen) |
|
|
dem Versetzungstyp (Schraube, Stufe, gemischt) |
|
|
den Symmetrien der beiden Ebenen (bei der
Kleinwinkel-Korngrenze sind beide noch gleich) |
|
Abbildung: |
|
|
Entstehung des
Schraubenversetzung-Netzwerks bei <100> Kleinwinkel-Drehkorngrenzen in
kubischen Kristallen |
|
|
Passende Netzebenenabbildung
zu obiger Abbildung
(Korngrenzenversetzungen in einer Twist
Kleinwinkelkorngrenze mit Tiltanteil |
|
|
(Muß noch beschriftet werden)) |
|
Die <100> Kleinwinkel-Drehkorngrenze in
Silizium, oder allgemein, in kubischen Kristallen ist, abgesehen von der
simplen symmetrischen KW-Kipp-KG, die einfachste KWKG, oder einfachste
"richtige" Korngrenze überhaupt. |
|
Die vierzählige Symmetrie in Verbindung mit
keinen Reaktionen an den Knoten der aufgespaltenen b=a/2<100>
Schraubenversetzungen (am Thompson Tetraeder nachvollziehen!) ergibt eine
simples quadratisches Versetzungsnetzwerk. |
|
Abbildung: |
|
|
Die <100>
Kleinwinkel-Drehkorngrenze in Silizium |
|
|
quadratisches Netzwerk gut erkennbar |
|
|
Abstand d der Versetzungen ergibt Drehwinkel mit Frank-Formel
 |
|
|
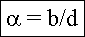"Störungen" (=extrinsische Versetzungen)
akkommodieren Stufen in der KG-Ebene (Facettierung in {100}) |
|
|
außerdem sichbar: SiO2 - Ausscheidungen vom
Herstellprozeß |
