 |
Zwei Grenzfälle: |
|
 |
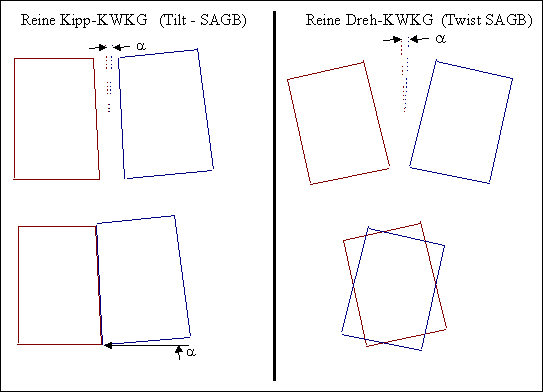
|
|
 |
In der gezeichneten Lage würde erst nach Drehung eines
Korns um a eine exakte low- S Orientierung vorliegen. Zusammenfügen wie
gezeichnet erzeugt damit Korngrenzen die nicht in einer exakten low-
S Orientierung liegen. |
|
 |
Energetisch günstiger kann die Einführung von
Korngrenzenversetzungen sein: |
|
|

|
| Eine "Wand" von Stufenversetzungen
ermöglicht die notwendige Anpassung |
|
Ein Netzwerk (nicht notwendigerweise quadratisch)
von Schraubenversetzungen ermöglicht die Drehung |
|
| |
|
|
 |
Damit besteht folgende Situation: |
|
 |
Zwischen den Versetzungen ist eine exakte "low
S-Orientierung" |
|
 |
Die gesamte Fehlpassung ist auf die Versetzungen
konzentriert |
|
 |
Damit einerseits Energieabsenkung zwischen den
Versetzungen, andererseits Energieerhöhung durch die Versetzungen
mit der Optimierung und damit Konsequenz: |
 |
Korngrenzen mit Korngrenzenversetzungen sind
für kleine Abweichungen von einer "low S-Orientierung" i.a. günstiger als Korngrenzen
ohne Versetzungen. |
|
 |
Die Burgersvektoren der Korngrenzenversetzungen sind
notwendigerweise Vektoren des zum Koinzidenzgitters gehörenden DSC
Gitters. |
 |
Frage: Wie wird das
CSL-Gitter und das zugehörige DSC-Gitter berechnet? |
|
 |
Allgemeiner Fall für Korngrenzen: Zwei sich
durchdringende Bravais Gitter des gleichen Typs (also auch z.B. trikline
Gitter) und identischer Gitterkonstante |
|
 |
Noch allgemeiner für Phasengrenzen: Zwei sich
durchdringende Bravais Gitter verschiedenen Typs und verschiedener
Gitterkonstanten (Dann müssen nicht notwendigerweise Lösungen, d.h.
Koinzidenzgitter existieren). |
 |
Antwort: Mit Mühe und nach W.
Bollmann:
"Crystalline Defects and Crystalline Interfaces", Springer 1970 |
|
 |
Einige Lösungen für fcc Kristalle |
|
|
| S |
Erzeugung |
b aus DSC-Gitter |
| 1 |
"Kleinwinkelkorngrenze" |
a/2 <110>, evtl. aufgespalten |
| 3 |
Zwillingskorngrenze |
a/6 <112>, a/3 <111> |
| 5 |
37° um <100> |
a/10 <130>, ... |
| 9 |
39,9° um <110> |
1/18<114>, 1/9<122>, 1/18<127>, |
| 19 |
26,5° um <110> |
a/38 <116>, a/19<133>, a/19 <10,9,3> |
| 41 |
12,7° um <100> |
a/82<41,5,4>, a/82<910>, ... |
|
 |
Man kann sich fragen, ob hohe S-Werte, wie der obige Wert von S=41, noch besonders sinnvoll sind. Die Antwort gibt das
Experiment: |
|
 |
Abbildung: TEM Aufnahme einer
S=41 Korngrenze mit Korngrenzenversetzungen des
Burgersvektors b=a/82 <41,5,4> in einem Abstand von 20nm
|
|
 |
Die "Streifung" ist eine Anordnung von
Korngrenzenversetzungen mit dem obigen Burgersvektor! Wie kann man das
feststellen? Mit Kontrastexperimenten wie bei Gitter-Versetzungen auch.
Korngrenzenversetzungen haben Spannungsfelder wie normale Versetzungen auch;
allerdings wegen dem viel kleineren Burgersvektor mit kleineren Beträgen.
Mir entsprechenden Simulationen kann man die Erscheinungsform (inkl.
Kontrastausslöschung, siehe Kap. 6.1) berechnen und mit den
realen Bildern vergleichen. |
|
 |
Viele solche Analysen wurden gemacht; sie zeigen eindeutig,
daß Korngrenzenversetzungen nicht nur existieren sondern auch noch alle
Reaktionen, die man von "normalenVersetzungen kennt, durchführen
können - inkl. der Aufspaltung in Partialversetzungen unter
Einschluß eines Stapelfehlers im DSC-Gitter! |


