|
|
 |
Wir wollen jetzt Korngrenzenversetzungen
einführen; d.h. sekundäre Korngrenzendefekte mit
Versetzungscharakter, die aber nur in der Korngrenze existieren können.
|
|
 |
Mit der Voltaterra Definition
machen wir erst einen Schnitt in der Ebene der Korngrenze (KG). |
|
 |
Dann erfolgt die Verschiebung einer Hälfte des Kristalls,
d.h. eines Korns, um einen Vektor der nicht die Strukur des Kristalls, sondern
die Struktur der KG erhält! Das
heißt z.B. das eine Koinzidienzorientierung erhalten bleibt. Es
heißt aber nicht, daß die Koinzidenzpunkte an der gleiche
Stelle bleiben müssen. |
|
 |
Der nötige Verschiebungsvektor muß nicht unbedingt
ein Gittervektor sein (obwohl das natürlich funktioniert), sondern kann
ein viel kleinerer Vektor sein. |
|
 |
Das Kriterium ist: Das CSL muß "vor"
und "hinter" der Versetzung erhalten bleiben; alle
Verschiebungen die das erreichen sind zugelassene Burgersvektoren für
Korngrenzenversetzungen.
|
 |
Die erlaubten Verschiebungsvektoren
(=bKG) spannen ein neues Gitter auf, das sogenannte DSC-Gitter.
(DSC steht für "Displacement Shift Complete") |
 |
Das DSC-Gitter ist schlicht das
"gröbste" Gitter, das im CSL-Gitter aufgespannt werden kann, und
bei dem alle Atome beider Körner auf DSC-Gitterpunkten sitzen
(konsequenterweise sitzen auf den meisten Gitterpunkten des DSC-Gitters dann
keine Atome). |
|
 |
Jede Verschiebung in diesem Gitter verschiebt nur den
Nullpunkt des CSL-Gitters, d.h. läßt die Struktur der KG
außerhalb des Versetzungskerns intakt. |
 |
Man versteht das am einfachsten durch Bilder:
Abbildung: Spielen mit dem Beispiel der S=5
Korngrenze aus dem vorhergehenden Kapitel (muß man noch mit
Folien machen) |
|
|
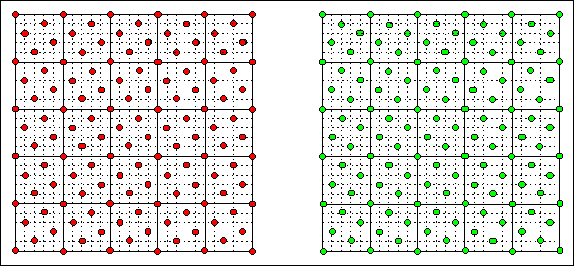
|
 |
Die ausgezogenen Linien entsprechen
offensichtlich dem CSL-Gitter; die gestrichelten Linien bilden offenbar das
DSC-Gitter, denn sie enthalten alle überhaupt möglichen
Atompositionen |
 |
Gezeigt ist eine S5
Situation; einige Regeln lassen sich erahnen: |
|
 |
Je größer die Elementarzelle des CSL-Gitters, desto
kleiner ist die Elementarzelle des DSC-Gitters. |
|
 |
Quantitativ: Für kubische Gitter ist das
DSC-Gitter das "reziproke" Gitter (im Ortsraum) des CSL-Gitters;
|
|
 |
Die Volumina von CSL-Gitter, Kristallgitter und DSC-Gitter
verhalten sich wie S : 1 : S -1für primitive kubische Kristalle
und wie S : 1 : 0,5 S -1 für bcc und fcc Kristalle. |
 |
Die Bedeutung von all diesen Gittern ist folgende:
|
|
 |
Korngrenzen, die in der Nähe einer
"low-S" Orientierung liegen, können
Energie gewinnen, wenn sie Korngrenzenversetzungen (mit Burgersvektor=Vektor
des DSC-Gitters) so bilden, daß die versetzungsfreien Teile der
Korngrenze jetzt exakt in der "low-S"
Orientierung liegen. |

