|
|
 |
In realen Kristallen enthalten Versetzungen in der
Regel Kinken und Jogs.
|
|
 |
Diese "Defekte im Defekt" beeinflussen sehr stark
die Beweglichkeit von Versetzungen. Ihre Entstehung kann mehrere Ursachen
haben; insbesondere entstehen sie auch durch die Bewegung selbst. |
 |
Natur der Kinken |
|
 |
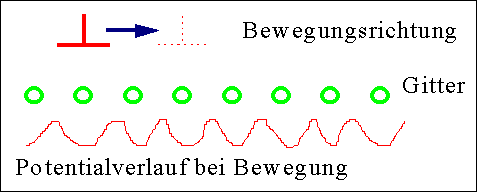
Vorbemerkung: Versetzungen in Kristallen (nicht bei
Voltaterra) liegen im Gleichgewicht im Minimum eines Energiepotentials, des
Peierls-Potentials |
|
 |
Veranschaulichung: |
|
|
|
|
 |
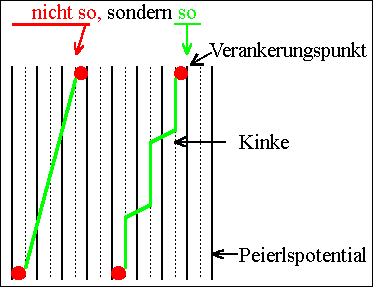
Dadurch gibt es ausgezeichnete Richtungen im Kristall, in denen die
Versetzungen liegen möchten. Eine Fast-Stufenversetzung, z.B. hat eine
kleinere Energie wenn sie zwischen zwei Verankerungspunkten möglichst
große Strecken als reine Stufenversetzung verläuft, also |
|
|
 |
 |
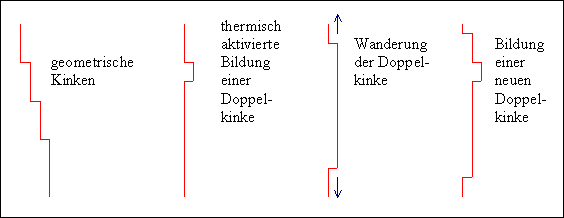
Es ist sinnvoll, zwischen geometrischen Kinken
(Wie im Bild oben) und Kinken im thermischen Gleichgewicht zu
unterscheiden. Letztere treten dann als Doppelkinken mit entgegengesetzten
Vorzeichen auf: |
|
|
|
 |
Kinken sind damit in dieser Definition
Sprünge atomarer Dimension in der Versetzungslinie, die auf der
Gleitebene liegen. |
|
 |
Auch Schraubenversetzungen liegen im Minimum eines
Peierls-Potentials und können Kinken haben. Die Kinke hat dann aber per
Definition Stufencharakter - als Konsequenz hat die gesamte
Schraubenversetzung jetzt auch eine Gleitebene, oder die Kinke wirkt als
Verankerungspunkt. |
|
 |
Durch thermisch aktivierte Bildung von Doppelkinken kann
Versetzungsbewegung auch unterhalb einer kritischen Scherspannung stattfinden,
d.h. bei wirkenden Kräfen tb,
die zu klein sind, um die Versetzung über die Peierls-Potentialbarriere zu
heben. |
 |
Der Effekt zeigt sich besonders schön in
Experimenten zur inneren Reibung. |
Jogs
|
 |
Natur der Jogs |
|
 |
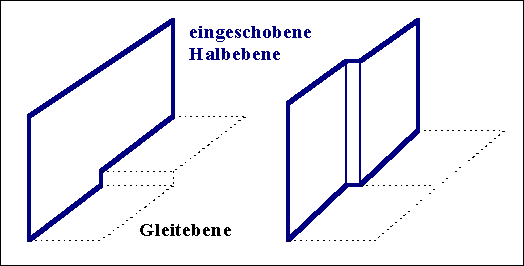
Jogs kann man als Oberbegriff auffassen, der alle
"Sprünge" in Versetzungslinien umfaßt (Kinken wären
dann die Teilmenge mit dem Sprung in der Gleitebene), oder - eingeschränkt
- als Sprünge außerhalb der Gleitebene. In eienm Bild das nur die
eingeschobene Halbebene einer reinen Stufenversetzung darstellt, sieht das so
aus: |
|
|
|
 |
Jogs eignen sich erkennbar gut als Keim zur
Anlagerung oder Emission von Atomaren Fehlstellen |
|
|
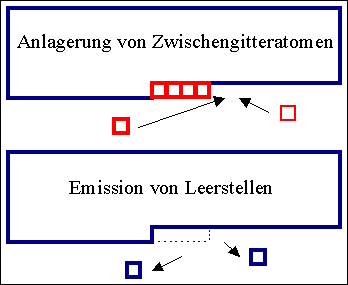 |
Auch durch Anlagerung oder Emission von atomaren Fehlstellen bewegt sich
die Versetzung. Dieser Prozeß heißt Klettern der Versetzung. |
|
 |
Ganz allgemein wird definiert: |
|
 |
Konservative Bewegung der Vesetzung=Bewegung ohne Beteiligung
von atomaren Fehlstellen=Bewegung in der Gleitebene=Gleiten |
|
 |
Nichtkonservative Bewegung=Bewegung aus Gleitebene
heraus=Beteiligung von atomaren Fehlstellen=Klettern |
| Entstehung von Kinken und Jogs
|
 |
Drei Mechanismen sind identifizierbar: |
|
 |
Thermisch aktivierte Bildung von Doppelkinken |
|
 |
Thermisch beeinflußte (z.B. wg. Übersättigung
von atomaren Fehlstellen) Bildung von Jogs durch Anlagerung / Emission von
atomaren Fehlstellen ("Diffusionssprünge") |
|
 |
Schneiden von Versetzungen |
 |
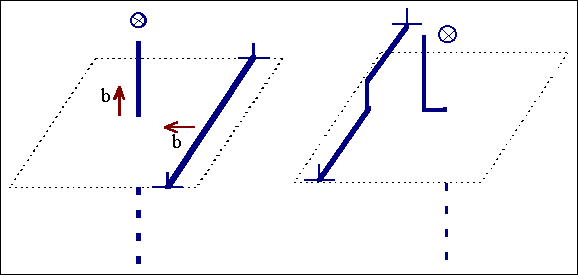
Der letztere Prozeß muß erklärt
werden. Wir betrachten die Bewegung einer Stufenversetzung in folgende
Geometrie: |
|
|
 |
|
 |
Durch das "Schneiden" der Stufen- mit der
Schraubenversetzung sind zwei Jogs entstanden. Auch beim Schneiden von
beliebigen Versetzungen entstehen immer Stufen. |
 |
Damit ergibt sich der allgemeine Bezug: |
|
 |
Versetzungsbewegung erzeugt Jogs, und |
|
 |
Jogs beeinflußen massiv die Beweglichkeit von
Versetzungen |
|
 |
Die Bewegung von Versetzungen kann "Debris"
hinterlassen, z.B. ganze Reihen von atomaren Fehlstellen, oder, wenn der Jog
über mehrere Netzebenen geht, kleine Versetzungsringe, weil der Jog bei
der konservativen Bewegung der Hauptversetzung klettern muß um
mitgeschleppt zu werden. |
|
 |
Abbildung:
Leerstellen-Erzeugung beim Gleiten einer
Schraubenversetzung mit Jogs |
| Erzeugung von Versetzungen
|
 |
Die Bewegung von Versetzungen erfolgt i.d.R. um
äußeren Kräften nachgeben zu können, d.h. plastische
Verformung des Kristalls zu ermöglichen. Dazu müssen erstmal
Versetzungen vorhanden sein; ist dies nicht der Fall, oder sind nur ganz wenige
da, muß ein Mechanismus zur Erzeugung von Versetzungen existieren. |
|
 |
Zunächst können Versetzungen an der
Kristalloberfläche entstehen; die Prinzipbilder zum Durchgang einer
Stufenversetzung (S. 5-2) zeigen dies schon. Wichtiger und komplizierter ist
die Versetzungsentstehung durch Versetzungsmultiplikation im Volumen. Der
relevante Mechanismus ist: Versetzungsmultiplikation durch den Frank- ReadMechanismus. |
|
|
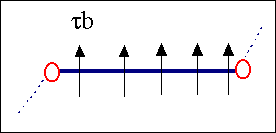 |
Versetzungssegment zwischen zwei Verankerungspunkten; Kraft
tb |
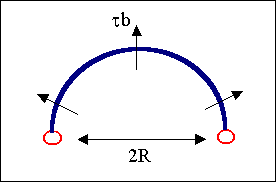 |
Ausbiegung zum Halbkreis mit Radius R erfordert die max. Spannung
tmax=Gb/R |
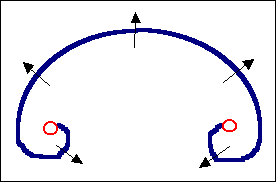 |
Der Krümmungsradius ist jetzt zu klein für die vorhandene
Spannung; die Versetzung ist instabil; der Ausbauchungsprozeß läuft
von allein weiter |
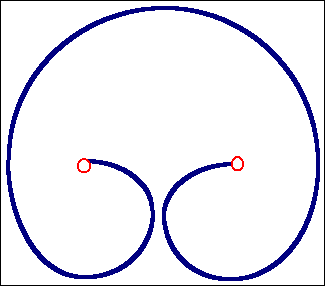 |
Die beiden Segmente die sich fast berühren haben entgegengesetzten
Burgersvektor (bei gleichem Linienvektor) und können sich auslöschen
|
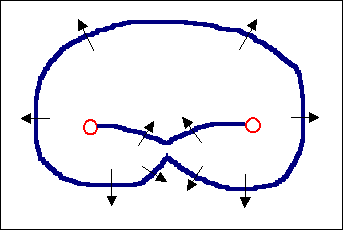 |
Es bildet sich ein Versetzungsring und ein wieder zwischen den
Verankerungspunkten aufgespanntes Versetzungsstück, hier in einer
völlig instabilen Lage gezeigt, die sofort (Gummifadenmodell!) in
die stabile Lage umschnappt. |
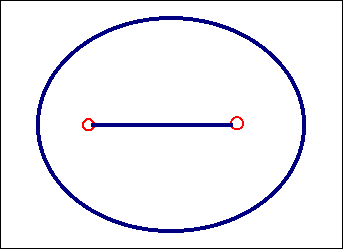 |
Stabile Lage: Der Versetzungsring wird bei weiterhin vorhandener
Kraft wachsen, und das Versetzungssegment wiederholt den Prozeß ad
infinitum. |
|
 |
Der Frank-Read Prozeß kann also die
Versetzungsdichte ins Beliebige erhöhen - natürlich wird er zum
Stillstand kommen, sobald die Primärversetzung z.B. Schneiden durch eine
andere Versetzung modifiziert wird. |
 |
Es gibt weitere, wesentlich kompliziertere
Mechanismen, die hier aber nicht näher behandelt werden sollen. |











