5.2.5 Wechselwirkung zwischen Versetzungen

	Zu untersuchen ist zunächst die Wechselwirkung zwischen parallelen Versetzungen.
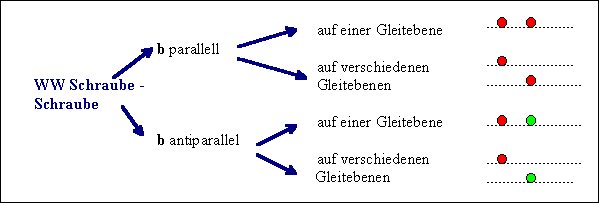
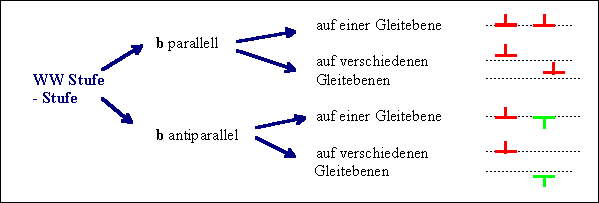
		Die wesentlichen Fallunterscheidungen sind
	Stufe - Schraube (analog zu obigen Geometrien) und daraus:
	Beliebige Versetzung - beliebige Versetzung
		Burgersvektor in Stufen- und Schraubenanteil aufspalten und Wechselwirkung getrennt betrachten
	Behandlung der obigen Fälle: Mit den Formeln für das Spannungsfeld einer Versetzung und der Kraftformel (auch als Peach-Köhler Formel bekannt), lassen sich alle obigen Fälle rechnen.
	Qualitativ lassen sich aber schon durch eine energetische Betrachtung die obigen Fälle klassifizieren. Wir benutzen im folgenden die obigen Symbole. Einfache Regeln:
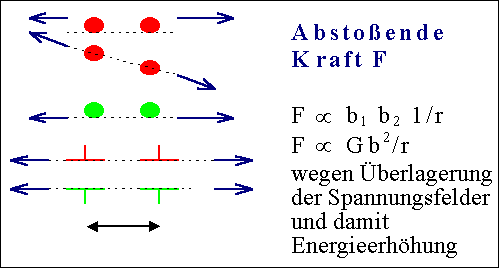
		Beliebige Versetzungen mit gleichem b auf einer Gleitebene stoßen sich im Allgemeinen ab.
		Beliebige Versetzungen mit entgegengesetzt gleichen b-Vektoren auf derselben Gleitebene ziehen sich an und vernichten sich.
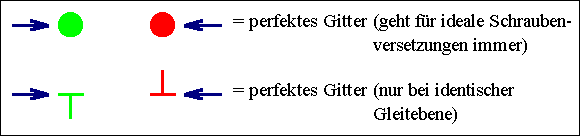
		Stufenversetzungen mit gleichen oder entgegengesetzten Burgersvektoren auf benachbarten Gleitebene ziehen sich an und stoßen sich ab, je nach Geometrie.
		Die allgemeine Formel für die Kraft zwischen Stufenversetzungen lautet für obige Geometrie
		Fx  =  Gb2 2p(1 –n)    ·  x · (x2 – y2) (x2 + y2)2 Fy  =  Gb2 2p(1 –n)    ·  y · (3x2 + y2) (x2 + y2)2
		Für y=0, d.h. dieselbe Gleitebene, ergibt sich das intuitiv angenommen 1/r- Gesetz.
		Für y < > 0 ergeben sich Zonen mit Anziehung und Abstoßung, siehe Abbildung.
		Für Fy existiert ein ähnlicher Ausdruck; da sich die Versetzung aber nicht in y-Richtung durch Gleitung bewegen kann, hat diese Kraft Komponente (zunächst) keine Relevanz
	Abbildung: Kraft auf Gleitebene (Fx) als Funktion von x (in Einheiten von y)
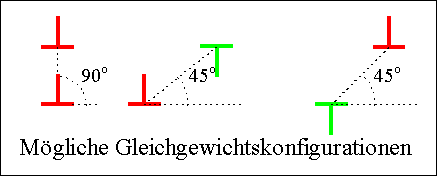
		Damit ergibt sich ein einfaches Bild für die Gleichgewichtsabstände