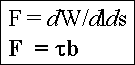|
|
 |
Wiederum sind detaillierte Berechnungen
kompliziert, für viele praktische Fälle läßt sich jedoch
eine simple Näherungsformel ableiten, am einfachsten durch eine
energetische Betrachtung |
|
 |
Zunächst muß man sich klar machen, daß
für die Versetzungsbewegung in der Gleitebene nur die Komponente der
Scherspannung in Gleitrichtung zählt. |
|
|
 |
|
 |
Unter dem Einfluß der dann auf die Versetzung wirkende
Kraft (die wir berechnen wollen) bewegt sich die Versetzung, dabei wird Arbeit
W=Kraft mal Weg geleistet. |
|
 |
Bei einer Gesamtfläche der Gleitebene von A und einem
kompletten Durchgang einer Versetzung mit Burgersvektor b, verschiebt
sich die obere Kristallhälfte gegenüber der unteren um b=Weg;
die wirkende Scherspannung ist t=(Kraft
F auf die Versetzung)/Fläche A |
|
 |
Damit wird die gesamte geleistete Arbeit W |
|
|
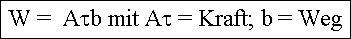
|
|
 |
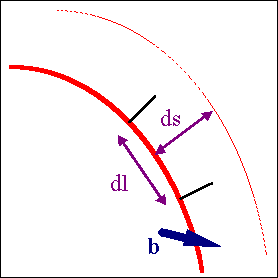
W setzt sich aus lauter differentiell zu betrachtenden
dW ´s zusammen, die z.B. als
dW=dlds betrachtet werden können |
|
|
|
Das Verhältnis der differentiell
geleisteten Arbeit zur gesamten
Arbeit ist damit=Gesamtfläche A
geteilt durch dlds
|
|
|
 |
Wir erhalten damit |
|
|
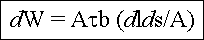
|
|
 |
und mit der Definition: Kraft F auf eine Versetzung
(pro Längeneinheit) |
|
|
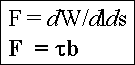
|
 |
Achtung! Hier sind nicht
nur Vorzeichen, sondern Richtungen ganz allg. sorgfältig zu betrachten
|
|
 |
Wichtig ist: t ist die in
der betrachteten Gleitebene herrschende Komponente der Scherspannung in
b-Richtung. Sie muß i.a. aus den gegebenen äußeren
Spannungen erst berechnt werden (z.B. durch Koordinatentransformation) |
 |
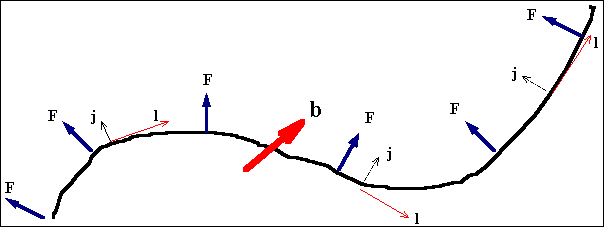
Kraft Fsteht immer senkrecht auf der
Versetzungslinie, auch bei überall konstantem t
|
|
|

|
 |
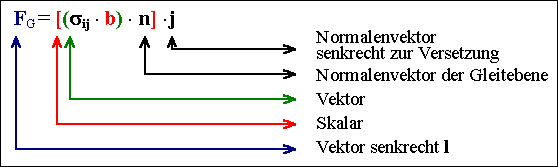
Die komplette Formel ist aufgrund der
Richtungen kompliziert und lautet: |
|
 |
F=(FN, FG)=Kraft als Vektor auf
Versetzung mit
FN, FG=Komponenten in der Gleitebene bzw.
senkrecht dazu, und |
|
|
|
|
|
 |
 |
Mit den Ausdrücken für die
Linienspannung bzw. -Energie und der "Kraftformel" läßt
sich eine wichtige Beziehung herleiten: |
|
 |
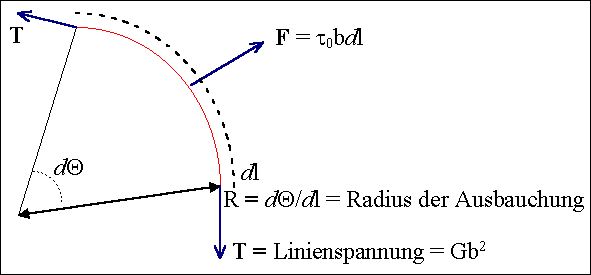
Notwendige Scherspannung, um eine Versetzung
"auszubauchen" |
|
|
 |
|
 |
Aus Kräftegleichgewicht: |
|
|
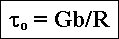
|
 |
Für das früher angesprochene
Versetzungsnetzwerk läßt sich ebenfalls eine neue Regel aufstellen:
|
|
 |
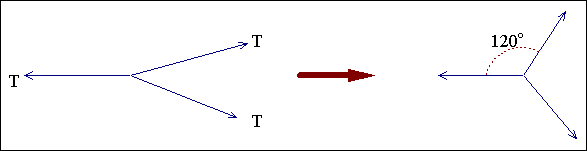
Die Summe der Linienspannung am Knoten muß Null sein,
sonst bewegt sich der Knoten. Damit werden alle (Dreier)-Knoten
näherungsweise Winkel von 120° aufweisen. |
|
|
 |
|
 |
Knoten mit mehr als drei Versetzungen werden sich in der Regel
zerlegen, um eine Minimalkonfiguration zu erreichen. Dabei ist aber die
Symmetrie der Veankerungspunkte, die Änderung der Linienenergie mit dem
Charakter, die Kristallanisotropie sowie die neue Gesamtlänge der
Versetzungen zu beachten: |