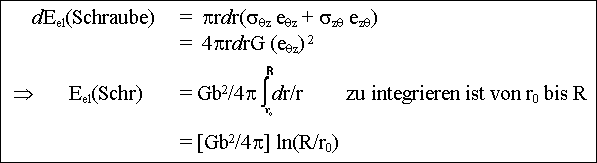
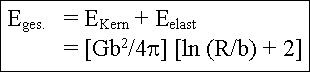
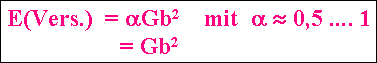
dies ist für die meisten Betrachtungen ausreichend.

(Frage: Was hält Versetzungringe stabil?)
| Mit den Ergebnissen der Elastizitätstheorie können näherungsweise die Linienenergie einer Versetzung und die (elastischen) Kräfte zwischen Versetzungen, mech. Spannungen und anderen Defekten berechnet werden. | ||
| Linienenergie einer Versetzung | ||
| Da die elastische Betrachtung für den Kernbereich der Versetzung nicht galt (in der "Röhre" des Zylinders), gilt für die gesamte in einer Versetzung gespeicherten Energie pro Längeneinheit | ||
| Die weiter oben gegebene Formel für die differentielle elastische Energie in einem Volumenelement führt bei Integration über das gesamte Volumen zur gesamten elastischen Energie. Die Integration ist für die Schraubenversetzung leicht durchführbar, im folgenden werden die Berechnungen pro Längeneinheit durchgeführt: | ||
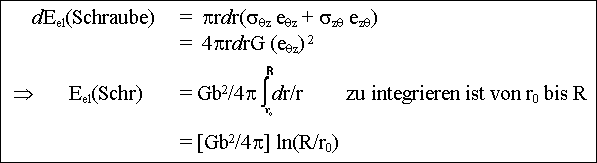 |
||
| mit R=äußerer Radius des Modellzylinders, sollte gegen Unendlich gehen, und r0 der innere Abschneideradius, in dem die Elastitzitätstheorie nicht angewendet werden kann. | ||
| Die Berechnung für die Stufenversetzung ist erheblich komplizierter, das Ergebnis ist jedoch wieder einfach: | ||
| Diskussion der Ergebnisse:Aus den beiden Formeln können eine Reihe von Schlüssen gezogen werden, sowie weitere Entwicklungen für brauchbare Näherungen abgeleitet werden: | ||
| 1. Die gesamte Energie ist der Versetzungslänge proportional: | ||
| Da grundsätzlich das Prinizip der Energieminimierung gilt, wird eine zwischen zwischen zwei Knoten verlaufende Versetzung dazu tendieren, als gerade Linie zu verlaufen | ||
| 2. Die Linienenergie einer Stufenversetzung ist immer größer als die einer Schraubenversetzung, da (1 - n) immer < 1 ist, d.h. um ungefähr den Faktor 3/2. Dadurch wird eine Versetzung dazu tendieren, einen möglichst hohen Anteil von Schraubenkomponenten zu haben (kann Punkt 1. widersprechen). | ||
| 3. Die elastische Linienenergie hängt (logarithmisch) von der Kristallgröße ab; im unendlich ausgedehnten Idealkristall ist sie Unendlich! Dies kann nicht sinnvoll sein, ist aber kein wirkliches Problem, denn unendlich ausgedehnte Kristalle gibt es nicht. Selbst in großen Kristallen ist allenfalls die lineare Dimension zu nehmen, jedoch eher die mittlere Entfernung zwischen Defekten, d.h. in der Regel Versetzungen, da sich die Spannungfelder im Mittel aufheben werden. | ||
| 4. Die elastische Linienenergie hängt ebenfalls logarithmisch vom Abschneideradius r0 ab. | ||
| 5. Beim ln (R/r0) geht R nur schwach
ein. Nimmt man für r0 eine sinnvollen Wert (z.B. 0.1 nm)
an und für R entweder 100 mm oder 1 mm, so ergibt sich für den
ln 13,8 bzw. 9,2. |
||
| Näherungen für brauchbare Formel | ||
| Der innerer Abschneideradius r0 wird mit dem Burgersvektor b gleichgesetzt. | ||
| Die Energie des Kernbereichs EKern mit Radius |b| wird gleich der Schmelzwärme gesetzt, d.h. der Energie die notwendig ist, um aus einem Kristall eine Flüssigkeit zu erzeugen. Eine noch bessere Näherung ist: | ||
| Die gesamte Energie wird dann | ||
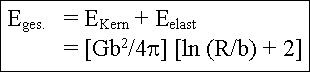 |
||
| Der ln- Ausdruck wird gerade 4p für R=3,88 x 104 |b|; d.h. für R c.a.=10 µm. Dies ist ein bißchen wenig, aber auch für R >> 10 µm ändert sich nicht viel. | ||
| Ganz allgemein gilt | ||
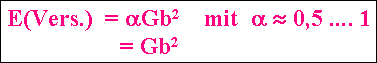
dies ist für die meisten Betrachtungen ausreichend. |
||
| Damit folgen weitere Eigenschaften | ||
| 6. Versetzungen haben immer den kleinstmöglichen Burgersvektor, da sonst eine Aufspaltung erfolgt: | ||
 |
||
| Da (b1)2 + (b2)2 < b2 ist, wird eine Aufspaltung immer energetisch günstig sein. Versetzungen mit "großen" Burgersvektoren gibt es nicht! | ||
| 7. Die Linienienergie liegt in der Größenordnung 5eV pro Burgersvektor. Damit sind Versetzungen immer Nichtgleichgewichtsdefekte; sie entstehen nicht "von allein" aus freien Energiegründen. | ||
| 8. Die hier betrachtete Linienenergie E ist identisch zu einer
Linienspannung, d.h. einer Kraft in Linienrichtung, die versucht die
Versetzung zu verkürzen. Dies folgt aus der Definition einer solchen Kraft
(F = dU/dL). Die Versetzung kann daher
modellmäßig als "Gummifaden" betrachtet werden, der
möglichst kurz sein will. (Frage: Was hält Versetzungringe stabil?) |
||