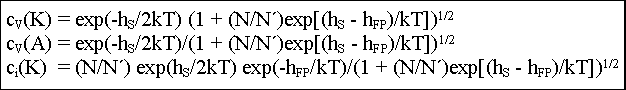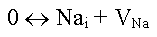2.2.2 Mehrere atomare Fehlstellen gleichzeitig: Gemischte Fehlordnung

	Wir betrachten das gleichzeitige Auftreten von Frenkel und Schottky Fehlordnung. Am einfachsten erschließt sich der allgemeine Fall aus dem Massenwirkungsgesetz. Dazu muß die Bildung der Fehlstellen als eine Reaktion im Gitter aufgefaßt werden, die in beide Richtungen laufen kann. Betrachten wir z.B. die Bildung eines Frenkel Paars im Kochsalz (NaCl). Es gibt zwei Möglichkeiten:
		Na hüpft auf einen Zwischengitterplatz, wir erhalten eine Na - Leerstelle (abgekürzt VNa) und ein Na- Zwischengitteratom (abgekürzt Nai)
		Cl hüpft ins Zwischengitter, usw.
	von denen nur die erste Variante relevant ist (die Anionen sind in der Regel zu groß, um auf eine Zwischengitterposition zu gehen).
	Man könnte nun naiverweise die Reaktion zur Bildung wie folgt annehmen:

		(falsch! falsch! falsch!)
	aber das ist falsch, denn "von nichts kommt nichts" - die Gleichung würde ja auch für den leeren Raum gelten. Irgendwie muß auch der Kristall berücksichtigt werden, in dem letztendlich die Defekte nur existieren können.
Der folgende Abschnitt ist im englischen Skript ausführlicher!
	Die richtige Formulierung schaut sich die Situation vorher und nachher genau an. Vor der Bildung des Frenkel Paars ist auf dem Platz, auf dem sich nachher die Na-Leerstelle befinden soll, ein Na-Atom, wir schreiben das NaNa, d.h. ein Na-Atom auf einem Na-Gitterplatz. Dort wo das Zwischengitteratom sich nachher befinden wird, ist vorher nichts. Da wir aber wissen, daß die mögliche Zwischengitteratom-Plätze auch ein Kristallgitter bilden (z.B. das Gitter der Oktaederlücken), können wir formal diese Situation als eine Leerstelle im Zwischengitter beschreiben, abgekürzt Vi (i für interstitiell). Die Reaktionsgleichung wird damit
		Das Massenwirkungsgesetz (MWG) sagt nun, daß
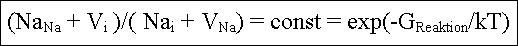		GReak ist natürlich mit der Bildungsenthalpie eines Frenkelpaars (hFP) gleichzusetzen. Mit NaNa=N=Zahl der Gitterplätze für Na und N´=Zahl der Zwischengitteratom - Plätze, und der üblichen Näherung, daß diese Zahlen konstant sind, erhält man für die Konzentrationen cV(A) der Anionen (Na) - Leerstelle und ci(A) des Anionen (Na) - Zwischengitteratoms die Gleichung
		Für die entsprechenden Schottky Defekte (Na und Cl-Leerstelle; gleich allgemein in Konzentrationen cV(A) und cV(K) ausgedrückt), ergibt sich
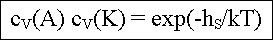		mit hS=Bildungsenthalpie eines Schottkypaars.
		Da Elektroneutralität vorausgesetzt ist (es kommen keine zusätzlichen Ladungen in den Kristall), muß gelten
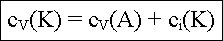
		neg. Ladungen=positive Ladungen
		Damit haben wir drei Gleichungen für die drei unbekannten Konzentrationen, deren Lösung einigermaßen simpel ist. Man erhält
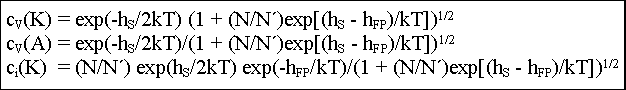
		Die reine Schottky- und Frenkel-Fehlordnung ist in diesen Formeln als Grenzfall enthalten.
Exercise 2.2.1 Do the math

	Bei der Übertragung dieses Ansatzes auf andere Systeme muß man ein bißchen aufpassen. Zum Beispiel ist die Konzentration der Leerstellen und Zwischengitteratome in Silizium (oder in jedem anderen Material, nur kommen dort Zwischengitteratome praktisch nicht vor) nicht durch die Reaktionsgleichung für Frenkelpaare beschreibbar, da beide Defekttypen unabhängig voneinander entstehen (an der Oberfläche oder an inneren Grenzflächen oder Versetzungen).
		Die jeweilige Gleichgewichts-Konzentration ist dann durch die simple Arrhenius-Beziehung gegeben, mit den individuellen Bildungsenthalpien.
		Die diversen Konzentrationen sind dann additiv
		Im Nichtgleichgewicht können durch gegenseitige Vernichtung oder andere Reaktionen jedoch Kopplungen eintreten - es wird ein lokales Gleichgewicht angestrebt.