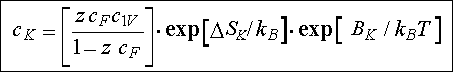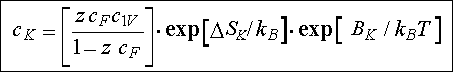 |
Alles was man über (eine Sorte) Fremdatome
in einem gegebenen Kristall wissen muß, folgt aus dem entsprechenden
Phasendiagramm. |
|
 |
Entscheidend ist die Löslichkeit als Funktion der Temperatur. In
erster Näherung (in der Regel nur über einen Bereich unterhalb evtl.
eutektischer Temperaturen erfüllt), ist die Gleichgewichtskonzentration an
atomaren Fremdatomen ("Dreck") auf Zwischengitteratomen oder
Gitterplätzen durch die allgemeine
Arrhenius-Beziehung
gegeben, die auch das Leerstellen- oder Zwischengitteratom-Gleichgewicht
beschreibt. Statt der Bildungsenergie und -Entropie müssen die
entsprechenden "Lösungs"energien und -entropien verwendet
werden. |
|
|
Im großen Unterschied zu Leerstellen und
Zwischengitteratomen sind die Fremdatomkonzentrationen in realen Proben eine
feste, experimentell praktisch nicht zu ändernde Größe, die
sich nicht im thermodynamischen Gleichgewicht selbst einstellen kann
(Fremdatome können nicht gebildet oder vernichtet werden). Das bedeutet,
daß in einem realen Kristall nur bei einer einzigen Temperatur (falls
überhaupt) Gleichgewicht bzgl. der Fremdatome herrschen kann - ansonsten
spricht man von Über- oder Untersättigung. |
|
Leerstellen, Doppelleerstellen, Zwischengitteratome usw.
können mit Fremdatomen Komplexe bilden, falls eine
anziehende Wechselwirkung besteht. Diese kann sowohl durch elastische (die
Gitterverzerrung eines großen Fremdatoms zieht Leerstellen an) als auch
durch elektrostatische Wechselwirkung zustandekommen (wenn Fremdatom und
Leerstelle im Kristall gegensätzlich geladen sind). |
|
|
Man kann ähnlich der vorhergehenden Rechnungen, z.B. die
Gleichgewichtskonzentrationen an Leerstellen-Fremdatompaaren ausrechnen, das
Ergebnis ist |
|
|
|
|
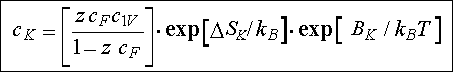
mit cF=Konzentration der Fremdatome
(Achtung: Änderung der Abkürzung; f
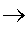c),cK=Konzentration der Fremdatom-Leerstellen Komplexe,
und SK bzw. BK die Bindungsentropie bzw.
-energie des Paars. z ist wieder die relevante Koordinationszahl, d.h.
die Anzahl der nächsten Nachbarn. |
|
Die gesamte
Leerstellenkonzentration(=Einfachleerstellen plus
Komplex-Leerstellenpaare (jedes enthält eine Leerstelle)) ist dabei |
|
|
 |
|
|
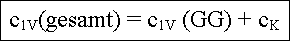Zu beachten ist, daß c1V die Konzentration der
Einfachleerstellen im perfekten Kristall (ohne Fremdatome) beschreibt, und
cK als Korrekturterm verstanden werden kann, der die
Änderung durch die Komplexbildung in Abhängigkeit von der
Fremdatomkonzentration beschreibt. Damit ist c1V >>
cK unterstellt. |
