5.2.2 Stress Field of a Straight Dislocation

Screw Dislocation

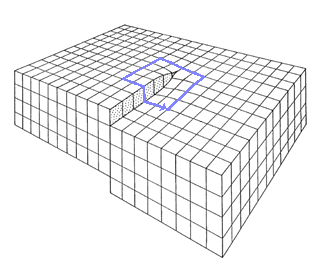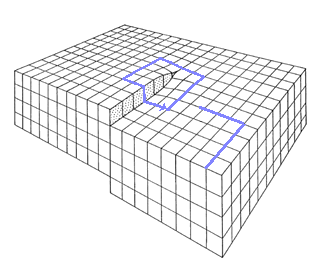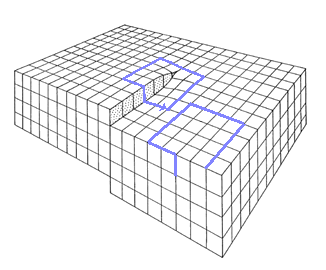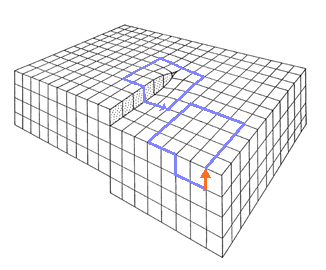
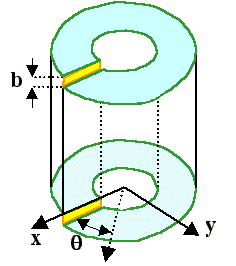
The elastic distortion around a straight screw dislocation of infinite length can be represented in terms of a cylinder of elastic material deformed as defined by Volterra. The following illustration shows the basic geometry.

A screw dislocation produces the deformation shown in the left hand picture. This can be modeled by the Volterra deformation mode as shown in the right hand picture - except for the core region of the dislocation, the deformation is the same. A radial slit was cut in the cylinder parallel to the z-axis, and the free surfaces displaced rigidly with respect to each other by the distance b, the magnitude of the Burgers vector of the screw dislocation, in the z-direction.

In the core region the strain is very large - atoms are displaced by about a lattice constant. Linear elasticity theory thus is not a valid approximation there, and we must exclude the core region. We then have no problem in using the Volterra approach; we just have to consider the core region separately and add it to the solutions from linear elasticity theory.

The elastic field in the dislocated cylinder can be found by direct inspection. First, it is noted that there are no displacements in the x and y directions, i.e. u_x=u_y=0 .

In the z-direction, the displacement varies smoothly from 0 to b as the angle q goes from 0 to 2p. This can be expressed as

u_z	=	b · q 2p	=	b 2p	· tan^–1(y/x)	=	b 2p	· arctan (y/x)

Using the equations for the strain we obtain the strain field of a screw dislocation:

e_xx	=	e_yy = e_zz = e_xy = e_yx = 0

e_xz	=	e_zx = –	b 4p	·	y x² + y²	= –	b 4p	·	sin q r

e_yz	=	e_zy =	b 4p	·	x x² + y²	=	b 4p	·	cos q r

The corresponding stress field is also easily obtained from the relevant equations:

s_xx	=	s_yy = s_zz = s_xy = s_yx = 0

s_xz	=	s_zx = –	G · b 2p	·	y x² + y²	= –	G · b 2p	·	sin q r

s_yz	=	s_zy =	G · b 2p	·	x x² + y²	=	G · b 2p	·	cos q r

In cylindrical coordinates, which are clearly better matched to the situation, the stress can be expressed via the following relations:

s_rz	=	s_xy cosq + s_yz sinq

s_{q z}	=	– s_xz sinq + s_yz cosq

Similar relations hold for the strain. We obtain the simple equations:

e_{q z}	=	e_zq =	b 4pr

s_{q z}	=	s_zq =	G · b 2pr

The elastic distortion contains no tensile or compressive components and consists of pure shear. s_z_q acts parallel to the z axis in radial planes of constant q and s_q_z acts in the fashion of a torque on planes normal to the axis. The field exhibits complete radial symmetry and the cut thus can be made on any radial plane q= constant. For a dislocation of opposite sign, i.e. a left-handed screw, the signs of all the field components are reversed.

There is, however, a serious problem with these equations:

The stresses and strains are proportional to 1/r and therefore diverge to infinity as r ® 0 as shown in the schematic picture on the left.

This makes no sense and therefore the cylinder used for the calculations must be hollow to avoid r - values that are too small, i.e. smaller than the core radius r₀.

Real crystals, of course, do (usually) not contain hollow dislocation cores. If we want to include the dislocation core, we must do this with a more advanced theory of deformation, which means a non-linear atomistic theory. There are, however, ways to avoid this, provided one is willing to accept a bit of empirical science.

The picture simply illustrates that strain and stress are, of course, smooth functions of r. The fact that linear elasticity theory can not cope with the core, does not mean that there is a real problem.

How large is radius r₀ or the extension of the dislocation core? Since the theory used is only valid for small strains, we may equate the core region with the region were the strain is larger than, say, 10%. From the equations above it is seen that the strain exceeds about 0,1 or 10% whenever r » b. A reasonable value for the dislocation core radius r₀ therefore lies in the range b to 4b, i.e. r₀ ³ 1 nm in most cases.

Edge Dislocation

The stress field of an edge dislocation is somewhat more complex than that of a screw dislocation, but can also be represented in an isotropic cylinder by the Volterra construction.

Using the same methodology as in the case of a screw dislocation, we replace the edge dislocation by the appropriate cut in a cylinder. The displacement and strains in the z-direction are zero and the deformation is basically a "plane strain".

It is not as easy as in the case of the screw dislocation to write down the strain field, but the reasoning follows the same line of arguments. We simply look at the results:

s_xx	= –	D · y	3x² + y² (x² + y²)²

s_yy	=	D · y	x² – y² (x² + y²)²

s_xy	=	s_yx =	D · x	x² – y² (x² + y²)²

s_zz	=	n · (s_xx + s_yy)

s_zz	=	s_zx = s_yz = s_zy = 0

We used the abbreviation D=Gb /2p (1 – n) .

The stress field has, therefore, both dilational and shear components. The largest normal stress is s_xx which acts parallel to the Burgers vector. Since the slip plane can be defined as y=0, the maximum compressive stress (s_xx is negative) acts immediately above the slip plane and the maximum tensile stress (s_xx is positive) acts immediately below the slip plane.

The effective pressure (given by the sum over the normal components of the stress) is

p	=	2 · (1 + n) · D 3	·	y x² + y²

We thus have compressive stress above the slip plane and tensile stresses below - just as deduced from the qualitative picture of an edge dislocation; graphical representation of the stress field of an edge dislocation is shown in the link.

For edge dislocations (and screw dislocations too), the sign of the stress- and strain components reverses if the sign of the Burgers vector is reversed.

Again, we have to leave out the dislocation core; the core radius again can be taken to be about 1b - 4b

We are left with the case of a mixed dislocation. This is not a problem anymore. Since we have a linear isotropic theory, we can just take the solutions for the edge- and screw component of the mixed dislocation and superimpose, i.e. add them.

As far as "simple" elasticity theory goes, we now have everything we can obtain. If better descriptions are needed, the matter becomes extremely complicated! But thankfully, this simple description is sufficient for most applications.