 |
| How can we obtain an arbitrary deformation of an arbitrary body by just repeating and combining some basic deformation prodedures? | |||
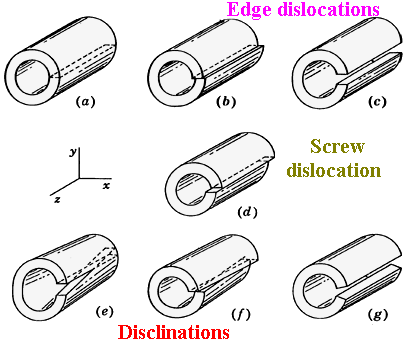
| The illustrations shows Volterras answer to this question: Take a cylinder of a material, cut it along some wall, shift the surfaces of the cut in all ways that - after welding the walls together again (including taking out or adding material) - will lead to different deformation states. | |||
| As Volterra showed, there is a limited and rather small number of possible independent cuts + shifts. All other cuts plus some deformation can always be expressed as a linear superposition of the elementary cuts. | |||
| Here are the elementary cuts. The first one just shows the cut, the next three ones correspond to dislocations - i.e. a real dislocation produces exactly the strain field generated by the cut and shift procedure. | |||
| |||
| The last three cuts corresponds to special defects called disclinations that are more elementary than dislocations, but are not observed in real crystals (except, maybe, in grain boundaries). They do however, appear in two-dimensional lattices, e.g. in the flux-line lattice of a superconductor. | |||
![]() 5.1.2 Volterra Construction and Consequences
5.1.2 Volterra Construction and Consequences
![]() 5.2.2 Stress Field of a Straight Dislocation
5.2.2 Stress Field of a Straight Dislocation
© H. Föll (Defects - Script)