 |
While the relation between the displacement field u(r)
and the local strain tensor eij is rather elementary, it does not hurt to recall
the decisive points. |
|
 |
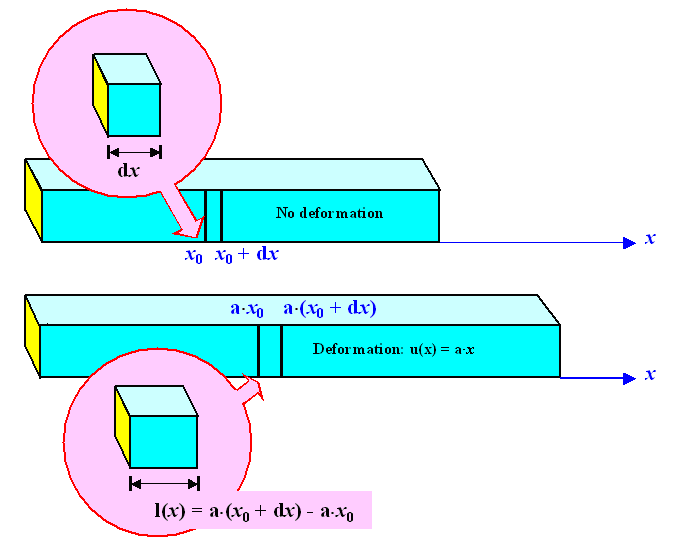
Let's take the simple example from the
backbone and consider a rod that is uniformly elongated; i.e. u(r)=ux(x)=a
· x; a is some constant. |
|
 |
In other words, the vector u
only has a component in x-direction, which only
depends on x as variable. The geometry than looks like this: |
| |
|
|
 |
At any point in the rod a little cube will be deformed into a cuboid - the side in x-direction is somewhat longer
than the others. |
 |
What kind of strain do we have to put on a cube positioned a x, to produce the cuboid?
|
|
 |
Well, since there is only strain in x-direction, we simply write down the elementary formula for strain |
| |
| exx |
= ex = |
l – l0
l0 |
= |
ux(x + dx) – ux(x)
dx | = |
dux
dx |
|
|
 |
If we deform in all three directions, we get corresponding expressions for eyy and ezz. |
 |
Since we also might have displacement components in x-direction
that depend on y or z, e.g. ux(x, y, z)=a · y,
we may, in general, also form mixed (partial) derivatives; e.g. ¶ux(x,
y, z)/¶y. What do those derivatives signify? |
|
 |
Shear stresses, of course. A little less easy to see, perhaps, but there can be no doubt about
it. |
|
 |
You may want to try to show that for yourself with the simple displacement field given above
and the equations in the backbone as a guideline for what
you are looking for. |
|
|
© H. Föll (Defects - Script)
![]() 5.2.1 Elasticity Theory, Energy and Forces
5.2.1 Elasticity Theory, Energy and Forces ![]() 5.2.2 Stress Field of a Straight Dislocation
5.2.2 Stress Field of a Straight Dislocation