4.2.1 Point Defects in Non-Equilibrium

4.2 Point Defects in Non-Equilibrium

The basic idea behind these techniques is simple: if you have more point defects than what you would have in thermal equilibrium, it should be easier to detect them. There are several methods, the most important one being quenching from high temperatures. Lets look at this technique in its extreme form:

A wire of the material to be investigated is heated to some desired (high) temperature T in liquid and superfluid He II (i.e. a liquid with a "¥" large heat conduction) to the desired temperature (by passing current through it). Astonishingly, this is easily possible because the He-vapor produced acts as a very efficient thermal shield and keeps the liquid He from exploding because too much heat is transferred.

After turning off the heating current, the specimen will cool extremely fast to He II temperature (» 1K). There is not much time for the point defects being present at the high temperature in thermal equilibrium to disappear via diffusion; they are to a large percentage "frozen-in". The frozen-in concentration can now be determined by e.g. measuring the residual resistivity r_res of the wire, the link gives an old example.

The residual resistivity is simply the resistivity found around 0 K. It is essentially dominated by defects because scattering of electrons at phonons is negligible.

There are, however, many problems with the quenching technique.

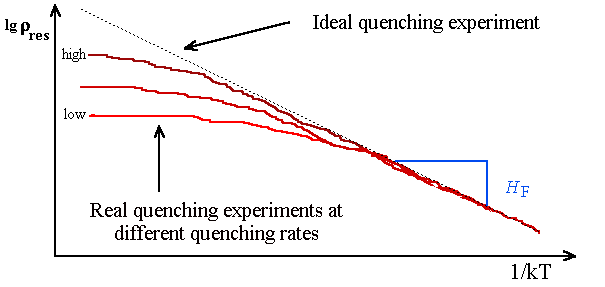
The quenching speed ( » 10⁴ ^oC/s with the He II technique) may still be too small to definitely rule out agglomeration off point defects (look at exercise 4.2-1). The cure for this problem is to repeat the experiments at different quenching speeds and to extrapolate to infinite quenching speed. What you will see for e.g. the residual resisitivity r_res may look like the schematic representation below.

We assumed in a fairly good approximation that r_res µ c_V; so we should get Arrhenius behaviour for r_res.

Recorded is the r_res in an Arrhenius plot as a function of the emperature T from which it was quenched. If you get a decent piece of a straigth line you can deduce the vacnacy formation enthalpy.

Plastic deformation is the next big problem.

The unavoidable large temperature gradients introduced by quenching produce large mechanical stress which may cause severe plastic deformation or even fracture of the specimen. Plastic deformation, in turn, may severley distort the concentrations of point defects and fracture of a sample simply terminates an experiment.

Finally, impurities, always there, may influence the results.

Since impurities may drastically influence the residual resistance, measurements with "dirty" specimens are always open to doubt. In addition, it is not generally easy to avoid in-diffusion of impurity atoms at the high temperatures needed for the experiment.

Quenching experiments with Si, for example, did not so far give useful data. If any "good" curves were obtained, it was invariably shown (later) that the results were due to impurity in-diffusion (usually Fe).

The illustration in the link gives an example for the processes occurring during quenching for Au obtained by calculations and demonstrates the difficulties in extracting data from raw measurements.

Exercise 4.2-1
Diffusion during cooling

	Other Methods

	If all else fails: try to find agglomerates of point defects looking at your specimen with the transmission electron microscope (TEM), with X-ray methods or with any other method that is applicable.
		Accept local equilibrium: Don't cool too fast, allow time for agglomerates to form. Conclude from the type of agglomerate, from their density and size, and whatever additional information you can gather, what kind of point defect with what concentration was prevalent.
		This is rather indirect and qualitative, but:
	It gives plenty of information. There are many examples where TEM contributed vital information to point defect research. Especially, it was TEM that gave the first clear indication that self-interstitials play a role in thermal equilibrium in Si and some rough numbers for formation energies and migration energies (Föll and Kolbesen 1978).
	In the link an example of the agglomerates of self-interstitials as detected by TEM is given. The major experimental problem in this case was to find the agglomerates. Their density is very low and at the required magnification huge areas had to be searched.


	A very new way of looking at point defects is to use the scanning tunneling microscope (STM) and to look at the atoms on the surface of the sample. This idea is not new; before the advent of the STM field ion microscopy was used with the same intention, but experiments were (and are) very difficult to do and severely limited.
		One idea is to investigate the surface after fracturing the quenched sample in-situ under ultra-high vacuum (UHV) conditions. This would give the density of vacancies on the fracture plane from which the bulk value could be deduced.
		An interesting set of STM images of point defects in GaAs from recent research is given in the link.
		Vacancies can be seen, but there are many problems: The image changes with time - the density of point defects goes up! Why - who knows?
		The interpretation of what you see is also difficult. In the example, several kinds of contrasts resulting from vacancies can be seen, probably because they are differently charged or at different depth in the sample (STM also "sees" defects one or two layers below the top layer). It needs detailed work to interprete the images as shown in the link.
		More recent pictures show the surface of Si or Pt, including point defects, in astonishing clarity. But we still will have to wait a few more years to see what contributions STM will be able to make towards the understanding of point defects.