Träger des Akademie-Preises für Physik 1976
Die Möglichkeit des kontrollierten Einbaus von Fremdatomen, wie z.B. Phosphor oder Bor, in das Kristallgitter des Siliziums ist die Grundlage der gesamten Halbleitertechnologie. Durch geeignete Wahl von Art und Konzentration dieser absichtlich erzeugten „Kristallbaufehler" (denn um solche handelt es sich) lassen sich die elektronischen Eigenschaften von Silizium, z.B. die elektrische Leitfähigkeit, in weiten Grenzen verändern. Zur Herstellung eines Bauelementes, beispielsweise eines Transistors, muß man in einem Kristall mehrere aneinandergrenzende Bereiche mit verschiedenem Gehalt an verschiedenen Fremdatomen erzeugen.
In Konkurrenz zu diesen „nützlichen" Kristallbaufehlern können die im Kristall schon von Anfang an enthaltenen Kristallbaufehler stehen. Diese „gewachsenen" Kristallbaufehler verändern die Eigenschaften des Materials oft unkontroIlierbar und sind deshalb generell unerwünscht. Bei der Zucht von Silizium-Einkristallen wird deshalb ein hohes Maß an Perfektion der Produkte verlangt; die stetig steigenden Anforderungen an die hergestellten Bauelemente bedingen ebenfalls ständig wachsende Ansprüche an die Perfektion der Ausgangskristalle.
Bevor wir auf eine spezielle Art von Kristallbaufehlern in Silizium näher eingehen – nämlich auf die sogenannten Swirl-Defekte – werden wir in einem eigenen Kapitel einige allgemeine für das Verständnis des folgenden wichtige Arten von Kristallbaufehlern vorstellen.
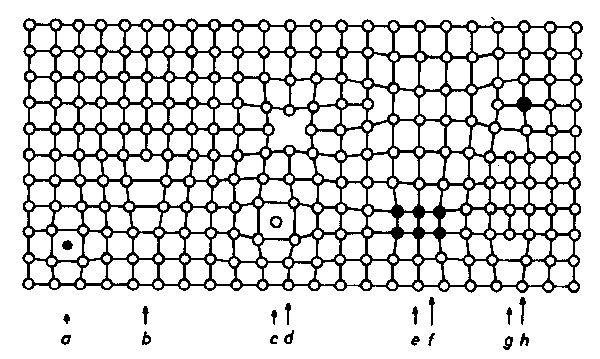
Fig. 1 zeigt schematisch einige wichtige Kristallbaufehler in Einkristallen: Versetzungen, atomare Fehlstellen, Fremdatome und Ausscheidungen von Fremdatomen. Versetzungen sind Störungen des Kristallgitters längs einer (gedachten) Linie, der Versetzungslinie. Fig. 1b veranschaulicht dies an Hand einer besonderen Versetzungsart, der sog. Stufenversetzung. Anzahl, Art und Eigenschaften der in einem Kristall vorhandenen Versetzungen bestimmen weitgehend dessen plastische Eigenschaften, d. h. Größen wie „Verformbarkeit", „Härte" und „Sprödigkeit". Versetzungen beeinflussen darüber hinaus noch die elektronischen Eigenschaften des Materials, insbesondere in Halbleitern. Unter atomaren Fehlstellen verstehen wir Leerstellen und Zwischengitteratome (Fig. 1c, d). Fremdatome (Fig. 1a, h) werden absichtlich in den Kristall eingebracht, gelangen aber auch unkontrolliert in das Kristallgitter. Die Agglomeration von atomaren Fehlstellen führt beispielsweise zu Versetzungsringen. Es gibt Versetzungsringe vom Leerstellen- (Fig. 1f) und vom Zwischengitteratomtyp (Fig. 1g). Ausscheidungen (Fig. 1c) von Fremdatomen entstehen durch die Agglomeration von Fremdatomen.

Fig. 1. Verschiedene Arten von Kristallbaufehlern, der Einfachheit halber in einem kubisch-primitiven Gitter dargestellt
a) Fremdatom auf einem Zwischengitterplatz. – b) Versetzung (sog. Stufenversetzung). Die Versetzungslinie verläuft senkrecht zur Zeichenebene. – c) Zwischengitteratom. – d) Leerstelle. – e) Ausscheidung von Fremdatomen. f) Versetzungsring vom Leerstellentyp (lokaler Unterschuß an Materie). – g) Versetzungsring vom Zwischengitteratomtyp (lokaler Überschuß an Materie). h) Fremdatom auf Gitterplatz; der im Sinne der Technologie „nützliche" Kristallbaufehler
Falls die aufgeführten Kristallbaufehler unkontrolliert vorhanden sind, ist ihr Einfluß auf die Eigenschaften des Siliziumkristalls ebenfalls unkontrollierbar, sie sind schädlich im Sinne der Technologie. Sie sind jedoch keineswegs grundsätzlich schädlich. Der erforderliche Einbau von Fremdatomen in das Silizium-Kristallgitter (das sog. Dotieren) kann z.B. nur unter der Mitwirkung von Leerstellen oder Zwischengitteratomen erfolgen, da ein Eindringen der Dotierstoffe in den Kristall (d.h. ihr Eindiffundieren) durch direkten Platztausch mit einem benachbarten Atom aus energetischen Gründen nicht möglich ist. (Dies gilt nur für Fremdatome, die auf einem regulären Gitterplatz sitzen, sog. substitutionelle Fremdatome. Das sind aber fast alle typischen Dotierungsstoffe.) Die Diffusion der Dotierungsatome erfolgt nach einem der in Fig. 2 veranschaulichten Mechanismen. Selbstverständlich können auch die Siliziumatome selbst durch einen dieser Mechanismen diffundieren, in diesem Falle spricht man von der Selbstdiffusion.
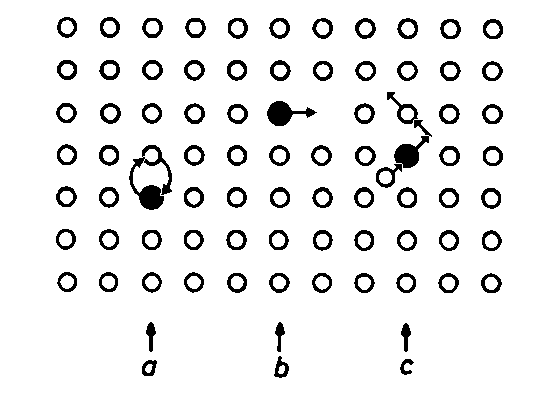
Fig. 2. Diffusionsmechanismen in Kristallen, dargestellt für Fremdatomdiffusion. Die Selbstdiffusion verläuft nach denselben Mechanismen
a) Direkter Platzwechsel. Aus energetischen Gründen nicht möglich. – b) Leerstellenmechanismus. Das Fremdatom kann einen Gitterplatz weiter springen, falls eine Leerstelle auf einen Nachbarplatz diffundiert ist. – c) (Indirekter) Zwischengitteratommechanismus. Ein Zwischengitteratom tauscht seinen Platz mit dem Fremdatom. Das dann auf einem Zwischengitterplatz sitzende Fremdatom springt sofort wieder auf einen Gitterplatz und erzeugt ein neues Zwischengitteratom
Die zur Diffusion erforderlichen atomaren Fehlstellen sind in jedem Kristall im thermischen Gleichgewicht vorhanden. Der Grund dafür ist, daß ein sich selbst überlassener Kristall (wie jedes abgeschlossene System) bestrebt ist, den Zustand kleinstmöglicher freier Energie (richtiger eigentlich: freier Enthalpie) anzunehmen. Dazu gehört aber nicht nur ein möglichst hoher Grad an Perfektion des Kristalls, sondern auch ein gewisses Maß an innerer „Unordnung", d.h. ein gewisses Maß an Entropie. Atomare Fehlstellen bringen dieses nötige Quantum Unordnung in den Kristall. Die Theorie zeigt, daß ihre Zahl mit steigender Temperatur exponentiell ansteigt. Die charakteristischen, ihre Konzentration bestimmenden Größen sind die Bildungsenergie EB und die Bildungsentropie SB Die Bildungsenergie ist ein Maß für die zur Erzeugung einer Fehlstelle notwendige Energie, sie liegt üblicherweise im Bereich 1 eV. Die Bildungsentropie liegt in der Größenordnung einer Boltzmannschen Konstanten; sie gibt ein ungefähres Maß dafür, wie weit eine Fehlstelle das sie umgebende Kristallgitter verändert.
Die Bildungsenergien für Leerstellen und Zwischengitteratome sind i.a. deutlich verschieden. Dies führt dazu, daß eine Sorte der atomaren Eigenfehlstellen weitaus überwiegt, nämlich die mit der kleineren Bildungsenergie. Die dominierende Fehlstellenart kontrolliert dann auch Selbst- und Fremdatomdiffusion.
Atomare Fehlstellen sind nicht unbeweglich im Kristallgitter fixiert, sondern können auf benachbarte Gitterplätze springen, sie führen eine Brownsche Bewegung aus. Die Zahl der Sprünge, die eine Fehlstelle pro Sekunde ausführt (oder ihr Diffusionskoeffizient), wächst exponentiell mit der Temperatur; die bestimmenden Größen für Sprungfrequenz bzw. Diffusionskoeffizient sind die Wanderungsenergie EW und die Wanderungsentropie SW.
Der Diffusionskoeffizient von Fremdatomen sowie der Selbstdiffusionskoeffizient hängen sowohl von der Konzentration der diffusionskontrollierenden Fehlstelle als auch von deren Diffusionskoeffizienten ab. Tatsächlich sind die charakteristischen Größen für die Selbstdiffusion, die Selbstdiffusionsenergie ESD und die Selbstdiffusionsentropie SSD, einfach die Summe aus Bildungs- und Wanderungsenergie bzw. Bildungs- und Wanderungsentropie der betreffenden Fehlstelle:
ESD =EW + EB, SSD=SW + SB.
Im thermischen Gleichgewicht dominiert in Metallen stets die Lehrstelle. Selbst- und Fremdatomdiffusion in Metallen erfolgen deshalb über einen Leerstellenmechanismus (Fig. 2b). Die Situation in Halbleitern, speziell in Silizium, ist komplizierter. Es grenzt nachgerade an ein Paradoxon, daß in demjenigen Element, in dem die Diffusion von Fremdatomen letztlich die Grundlage für eine Industrie mit Millionen von Beschäftigten und Milliarden an Jahresumsätzen darstellt, der Diffusionsmechanismus bis heute noch umstritten ist. Ein normaler Leerstellenmechanismus, der vielfach in Analogie zu Metallen angenommen wurde, kann nicht vorliegen, da die Summe der aus mehreren unabhängigen Experimenten gewonnenen Werte für ELB und ELW, nicht mit der Selbstdiffusionsenergie ESD übereinstimmen (der Index L steht für Leerstelle). Einen Ausweg aus dieser Schwierigkeit erhoffte man sich durch die Annahme von komplizierten Leerstellenmechanismen; keiner der vielen in die Diskussion eingebrachten Vorschläge konnte jedoch befriedigen (siehe z.B. [1]). Eine Lösung des Problems könnte erreicht werden, wenn man annimmt, daß nicht wie üblich die Leerstelle, sondern das Zwischengitteratom in Silizium die diffusionsbestimmende atomare Fehlstelle ist. Dieser unkonventionelle Vorschlag wurde erstmals 1968 von A. SEEGER und M. L. SWANSON [2] in die Diskussion eingebracht und in nachfolgenden Arbeiten detailliert ausgeführt [8, 4].
Aus dieser Hypothese folgt, daß in Silizium bei höheren Temperaturen nicht wie in Metallen Leerstellen, sondern Zwischengitteratome die dominierenden atomaren Fehlstellen im thermischen Gleichgewicht sind. Hier kann eine experimentelle Entscheidung zwischen den konkurrierenden Diffusionstheorien ansetzen: Gelingt es zu zeigen, welche Fehlstellenart im thermischen Gleichgewicht dominiert, kann daraus auf den Diffusionsmechanismus geschlossen werden.
Kristallbaufehler in Silizium zeigen also zwei Gesichter: Sie werden zur Herstellung von Bauelementen benötigt, können sich dabei aber auch schädlich auswirken. Das Ziel ist deshalb die Herstellung möglichst perfekter Kristalle und eine genaue Kenntnis der Eigenschaften der Kristallbaufehler, um sie kontrolliert einsetzen zu können.
Im Jahre 1958 gelang es W. C. DASH erstmals, große versetzungsfreie Kristalle zu züchten – ein Meilenstein in der Herstellung immer perfekterer Silizium-Einkristalle [5]. Halbleiterbauelemente werden heutzutage weitgehend aus solchen Kristallen gefertigt. Überraschenderweise trat in diesen Kristallen eine vorher nicht beobachtete neue Art von Defekten auf, die sog. Swirl-Defekte [6]. Vom technologischen Standpunkt aus sind sie zu den schädlichen Defekten zu rechnen. Wir beschränken uns auf die Diskussion dieser Defekte in sog. zonengezogenem Silizium. Bei diesem Kristallzuchtverfahren wird eine dünne Schmelzzone langsam in Achsenrichtung durch einen senkrechtstehenden polykristallinen Siliziumstab gezogen. Durch Einbringen eines kleinen „Impfkristalls" in den unteren, zuerst erstarrenden Teil der Schmelze wächst der sich neu bildende Kristall einkristallin. Der frischgezogene Einkristall kühlt allmählich ab; die Abkühlgeschwindigkeit ist um so größer, je schneller der Kristall „gezogen" wurde.
Zum Nachweis und zur Erforschung der Swirl-Defekte wurden bisher hauptsächlich drei Methoden verwendet. Es sind dies die Ätztechnik, die Röntgentopographie und die Durchstrahlungselektronenmikroskopie.
Swirl-Defekte können mit einer bestimmten Ätzlösung sehr leicht nachgewiesen werden, siehe z.B. [7]. Am Ort eines Swirl-Defektes bildet sich schon nach kurzem Eintauchen des (vorher spiegelblank polierten) Kristalls ein kleiner Hügel oder ein kleines Grübchen, die beide im Lichtmikroskop gut sichtbar sind. Fig. 8 zeigt das Ätzmuster der Swirl-Defekte auf einer senkrecht zur Wachstumsrichtung des Kristalles herausgeschnittenen Scheibe. Die deutlich zu erkennende spiralige Anordnung der Ätzhügel oder Grübchen (im Bild als kleine weiße Punkte sichtbar) gab Anlaß zu dem Namen „Swirl", zu deutsch etwa „Wirbel", „Strudel".
Ähnliche Informationen. wie die Ätztechnik liefert auch die sog. Röntgentopographie nach einer speziellen Vorbehandlung der Präparate. In der Vergangenheit war diese Methode sogar die Hauptuntersuchungsmethode. Zu erwähnen ist vor allem das für die Swirl-Erforschung grundlegende Werk von A. J. R. DE KOCK [8]. Aus Gründen der Übersichtlichkeit gehen wir auf diese Technik jedoch nicht näher ein.
Die wichtigsten mit diesen Methoden gewonnenen Ergebnisse sind:
1) Es gibt zwei Arten von Swirl-Defekten, die sich deutlich unterscheiden (z.B. in der Größe der Ätzgruben). In Anlehnung an DE KOCK [8] werden die größeren A-Defekte, die kleineren B-Defekte genannt.
2) Swirl-Defekte treten nur in Kristallen auf, die nicht schneller als mit ca. 4,5 mm/min [9], aber auch nicht langsamer als mit ca. 0,5 mm/min gezogen wurden [10]. Der für Auftreten oder Nicht-Auftreten verantwortliche Parameter ist die mit der Ziehgeschwindigkeit gekoppelte Abkühlgeschwindigkeit.
3) Der Gehalt des Kristalls an Sauerstoff, besonders aber an Kohlenstoff beeinflußt das Erscheinungsbild der Swirls: Kristalle mit sehr kleinem Gehalt an diesen Verunreinigungen enthalten keine B-Defekte und relativ wenig A-Defekte [11].
Ätztechnik und Röntgentopographie können kaum Aussagen über die mikroskopische Natur der Defekte erbringen; dies ist die Domäne der Elektronenmikroskopie. Ihrer Anwendung standen jedoch lange Zeit entscheidende experimentelle Schwierigkeiten im Wege.

Fig. 3. „Swirl" -Muster von Ätzgrübchen auf einer Siliziumscheibe
Präparate für die Elektronenmikroskopie müssen naturgemäß für den Elektronenstrahl transparent sein. Bei Verwendung eines konventionellen Elektronenmikroskopes mit etwa 100 kV Beschleunigungsspannung der Elektronen bedeutet dies, daß die Präparate nicht dicker als ca. 0,8 µm sein dürfen.
a)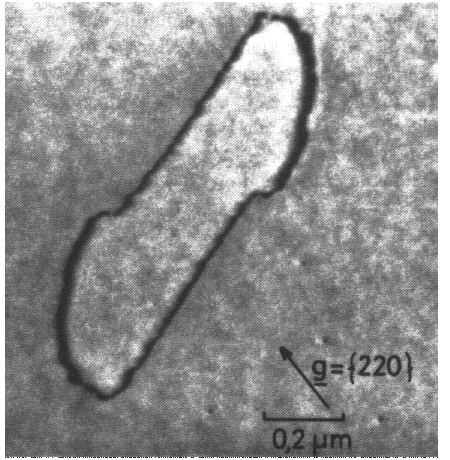
b)
Fig. 4. Zwei Beispiele von einfachen Versetzungsringen
a) Versetzungsring ohne Stapelfehler.
b) Versetzungsring mit Stapelfehler. Der Stapelfehler äußert sich durch einen dunklen Flächenkontrast
Derart dünne Präparate werden normalerweise durch chemisches Abpolieren dickerer Ausgangsproben hergestellt. Die dabei entstehenden durchstrahlbaren Gebiete (meistens die Ränder durchgeätzter Löcher) haben i.a. nur eine Fläche von einigen 10000 µm2. Die Dichte der Swirl-Defekte in einem ca. 1µm dicken Präparat ist ca. 1 Defekt auf 10000 µm2. Die Chance, im durchstrahlbaren Gebiet überhaupt einen Defekt zu finden, ist also klein. Darüber hinaus greift die Polierlösung den Siliziumkristall bevorzugt dort an, wo ein Swirl-Defekt enthalten ist. Falls also zufällig einmal ein Defekt im durchstrahlbaren Bereich des Präparates läge, wird er beim Polieren weggeätzt.
Diese Schwierigkeiten machten es praktisch unmöglich, Swirls mit Hilfe der konventionellen Elektronenmikroskopie zu untersuchen. Erst die Kombination einer speziell entwickelten Präparationstechnik mit der Hochspannungselektronenmikroskopie ermöglichte systematische Untersuchungen. Solche Mikroskope mit Beschleunigungsspannungen bei 1 MV und höher werden seit einigen Jahren hergestellt. Bedingt durch ihre hohen Anschaffungs- und Betriebskosten sind jedoch weltweit nur wenige dieser Geräte im Einsatz (in Deutschland zwei). In dem von uns benutzten Hochspannungsmikroskop, das bei einer Strahlspannung von 650 kV betrieben wurde, können bis zu ca. 5 µm dicke Präparate durchstrahlt werden; das Problem des Herausätzens der Defekte spielt bei Proben dieser Dicke keine große Rolle mehr. Ein von K. MAYER und L. BERNEWITZ entwickeltes Ätzverfahren ermöglichte es, die Swirl-Defekte zerstörungsfrei zu lokalisieren (durch die Bildung von Ätzhügeln anstatt von Ätzgrübchen) [12]. Durch ein speziell zur Untersuchung der Swirls entwickeltes Präparationsverfahren gelang es, beliebig ausgedehnte Präparate im Dickenbereich 1 – 5 µm, entnommen aus definierten Stellen des Kristalls, herzustellen [13]. Damit war die Voraussetzung für eine systematische mikroskopische Erforschung der Swirl-Defekte geben.
Die A-Defekte wurden als Versetzungsringe, oder als mehr oder weniger komplizierte Anhäufungen von Versetzungsringen identifiziert [14], die im folgenden pauschal als „Swirl-Ringe" bezeichnet werden. Fig. 4 und Fig. 5 zeigen einige typische elektronenmikroskopische Bilder. Man kann die Swirl-Ringe grob in drei Gruppen einteilen [15]:
1) Einfache Versetzungsringe; die einfachste Art der gefundenen Defekte. Auf ihre Geometrie und auf die Entstehung ihres elektronenmikroskopischen Kontrastes wird noch eingegangen.
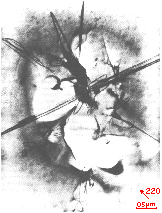
2) Agglomerate von Versetzungsringen und komplizierte Strukturen. Aus geometrischen Gründen muß auch diese Art der Swirl-Ringe aus mehreren, eventuell aus sehr vielen einzelnen Versetzungsringen entstanden sein. Durch Reaktionen der Versetzungen untereinander und durch mannigfaltige Möglichkeiten der Versetzungsbewegung entstehen die gezeigten komplizierten Strukturen (Fig. 5).
 (390 kB) |
Fig. 5. Komplizierter, aus vielen einfachen Versetzungsringen zusammengesetzter Swirl-Ring |
3) Versetzungsringe, die noch einen sog. Stapelfehler enthalten. Ein Beispiel ist in Fig. 4b gezeigt. Der Stapelfehler äußert sich in einem typischen Flächenkontrast innerhalb des Versetzungsringes. Bei einem Versetzungsring mit Stapelfehler ist das Kristallgitter nicht nur längs der Versetzungslinie gestört, sondern in charakteristischer Weise auch in der Ebene des Ringes; dies wird später noch näher ausgeführt.
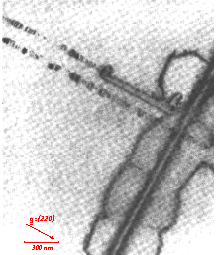
Obwohl sich Swirl-Ringe im Aussehen erheblich unterscheiden können, gibt es einige allen gemeinsame Merkmale. Neben ähnlichen geometrischen Besonderheiten ist besonders auffällig, daß die Versetzungslinien der Swirl-Ringe häufig sehr breit und ausgefranst erscheinen, oder daß sie mit einer Reihe von kleinen schwarzen Punkten umsäumt sind. Dies läßt darauf schließen, daß sich in unmittelbarer Nähe der Versetzungslinie noch zusätzliche Kristallbaufehler befinden, d.h. die Versetzung ist „dekoriert". Normalerweise sind diese Dekorationsdefekte zu klein, um im Elektronenmikroskop eindeutig identifiziert werden zu können. Dies gelang nur bei einigen Swirl-Ringen mit besonders ausgeprägter Dekoration. Fig. 6 zeigt, daß die Dekorationsdefekte wiederum kleine Versetzungsringe sind (Durchmesser ( <=30 nm), die entlang der Versetzungslinie aufgereiht sind.
Ein Elektronenstrahl kann als Materiewelle beschrieben werden (Wellenlänge bei 650 keV Energie 1.2·10-3 nm). Durchläuft er ein streng geordnetes Medium, z.B. einen Kristall, so treten Beugungseffekte auf. Diese äußern sich darin, daß für einen ganz bestimmten Winkel zwischen einer Netzebenenschar und dem Elektronenstrahl eine starke Reflexion des Elektronenstrahls an dieser Netzebenenschar auftritt. Als Netzebenen bezeichnet man die mit Atomen belegten (gedachten) Ebenen in einem Kristall; z.B. die Seitenflächen des Elementarwürfels in einem kubischen Kristall. In Fig. 7a ist eine Netzebenenschar durch Linien angedeutet, der richtige Winkel für starke Reflexion des Elektronenstrahls (der sog. Bragg- Winkel) sei eingestellt. Aus dem Kristall treten deshalb zwei Elektronenstrahlen aus, der Primärstrahl und ein intensiver abgebeugter Strahl, der einen beträchtlichen Teil der Elektronen enthalten kann. Da (in der sog. Hellfeldabbildung) nur der Primärstrahl zum Bild beiträgt, ist das Bild relativ dunkel. Wir betrachten nun einen Kristall, der eine Versetzung enthält (Fig. 7b). Der Kunstgriff zur Abbildung dieser Versetzung besteht darin, den Bragg-Winkel nicht exakt, sondern mit einer kleinen, definierten Abweichung einzustellen. Im ungestörten Kristall gehen jetzt nur wenige Elektronen durch Streuung in den abgebeugten Strahl verloren, das Bild ist relativ hell. Auf einer Seite der Versetzung sind, wie ein Vergleich mit Fig. 7a zeigt, die Netzebenen jedoch lokal in Richtung auf die exakte Bragg-Orientierung gebogen. Aus dieser Kristallregion werden also viele Elektronen in den abgebeugten Strahl gestreut; die Versetzung erscheint deshalb als dunkle Linie auf hellem Hintergrund. Bemerkenswert ist, daß das Kontrastbild einer Versetzung nicht am Ort ihrer geometrischen Projektion liegt, sondern nach links oder nach rechts verschoben ist. Das Vorzeichen dieser Kontrastverschiebung hängt von der Art der Versetzung und von den Abbildungsbedingungen ab.
 (430 kB) |
Fig. 6. Ausschnitt aus einem komplizierten Swirl-Ring. Die dekorierten Versetzungen sind bei den gewählten Abbildungsbedingungen unsichtbar, die die dekorierenden kleinen Versetzungsringe sind deutlich zu sehen |
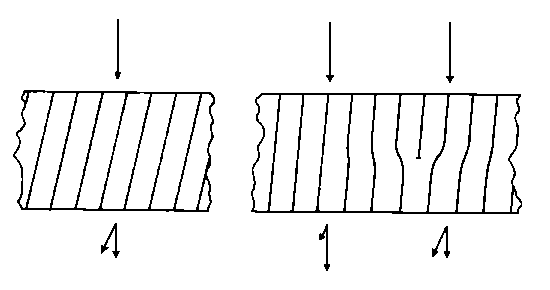
Fig. 7. Kontrastentstehung bei der Elektronenmikroskopie von Gitterbaufehlern am Beispiel einer Versetzung
a) Perfekter Kristall, genau in die Bragg-Lage orientiert. Ein intensiver abgebeugter Strahl verläßt den Kristall, der Primärstrahl ist entsprechend geschwächt. – b) Der Kristall ist etwas aus der Bragg-Lage herausgekippt. Rechts der Versetzung ist die Bragg-Bedingung lokal annähernd erfüllt, der abgebeugte Strahl ist dort intensiv. Die Versetzung erscheint als dunkle Linie auf hellem Untergrund rechtsvon ihrer eigentlichen geometrischen Position
Fig. 8. Kontrastentstehung an Versetzungsringen. Die für den Kontrast verantwortlichen Netzebenen sind gestrichelt gezeichnet. Der Vergleich mit Fig. 5b zeigt, daß in diesem Beispiel für den Versetzungsring vom Zwischengitteratomtyp der Kontakt innerhalb, für den Versetzungsring vom Leerstellentyp außerhalb der Ringprojektionen liegt
Fig. 8 verdeutlicht die Kontrastentstehung an Versetzungsringen; wir unterscheiden zwischen Versetzungsringen vom Leerstellen- und vom Zwischengitteratomtyp. Durch Vergleich mit Fig. 7 erkennt man sofort, daß im Falle des Leerstellenringes der Kontrast außerhalb, im Falle des Zwischengitteratomversetzungsringes innerhalb der Ringprojektion liegt. Es ist nun verhältnismäßig einfach festzustellen, ob ein „Außen"- oder ein „Innenkontrast" vorliegt. Bestimmt man zusätzlich noch die Ringebene, so läßt sich der Ringtyp vollends ermitteln. Eine detaillierte Beschreibung der Methode, die auch auf die bei komplizierteren Ringstrukturen eventuell eintretenden Komplikationen eingeht, findet sich in [16] und [17].
Mit der im vorhergehenden Abschnitt geschilderten Methode haben wir eine Vielzahl von einzelnen Versetzungsringen, von erkennbaren Versetzungsringen in komplizierteren Strukturen sowie – soweit sichtbar – von kleinen Versetzungsringen analysiert. In jedem Fall ergab sich, daß die Versetzungsringe vom Zwischengitteratomtyp waren [15]. P. PETROFF und A. J. R. de KOCK kamen unabhängig und praktisch gleichzeitig im wesentlichen zum selben Ergebnis, ihre Untersuchung war jedoch auf einige wenige Ringe mit einfacher Geometrie beschränkt [18].
Versetzungsringe, die einen Stapelfehler enthalten, können mit einer zweiten, von der ersten völlig unabhängigen Methode analysiert werden; auch hier ergeben sich ausschließlich Versetzungsringe vom Zwischengitteratomtyp [15].
Unmittelbar nach dem Erstarren der Schmelze zum Kristall ist eine relativ große Zahl an atomaren Fehlstellen im thermischen Gleichgewicht vorhanden. Beim Abkühlen nimmt die für den Kristall optimale Zahl an Fehlstellen, d.h. die thermische Gleichgewichtskonzentration, rasch ab. Soll der Gleichgewichtszustand eingehalten werden, müssen die im Überschuß vorhandenen Fehlstellen „ausheilen". Atomare Fehlstellen heilen i.a. so aus, daß die überschüssigen Fehlstellen zu sog. „Senken" diffundieren und dort absorbiert werden. Solche Senken sind beispielsweise die Kristalloberfläche, Korngrenzen und Versetzungen. In versetzungsfreien Kristallen, die so groß sind, daß die Oberfläche als Senke keine Rolle mehr spielt, können die atomaren Fehlstellen nicht auf die beschriebene Weise ausheilen. Statt dessen lagern sie sich zu sogenannten Fehlstellenagglomeraten zusammen. Alle diese Voraussetzungen treten auf Kristalle zu, die Swirl-Defekte enthalten. Diese Defekte werden deshalb übereinstimmend als die Agglomerate der bei hohen Temperaturen vorhandenen Fehlstellen interpretiert.
Die elektronenmikroskopische Untersuchung hat gezeigt, daß diese Fehlstellenagglomerate Versetzungsringe vom Zwischengitteratomtyp sind. Wir wollen den prinzipiellen Mechanismus der Entstehung von Versetzungsringen durch Agglomeration atomarer Fehlstellen nun näher betrachten. Fig. 9 zeigt diesen Prozeß schematisch. In einem nicht kubisch-primitiven Gitter, also auch im Diamantgitter des Siliziums, wird durch Anhäufung von Zwischengitteratomen zunächst ein Versetzungsring mit Stapelfehler auf der am dichtesten mit Atomen bepackten Netzebene gebildet (Fig. 9b). Mit wachsender Größe des Versetzungsringes durch Anlagerung weiterer Fehlstellen wird der Stapelfehler energetisch ungünstiger. Er wird dann in der Regel durch einen sog. Scherprozeß beseitigt (Fig. 9c). Unsere Untersuchungen zeigen, daß Swirl-Ringe durch Agglomeration von Silizium-Zwischengitteratomen entstehen. Die beschriebenen Experimente sind der erste direkte Nachweis für das Vorhandensein von Zwischengitteratomen in Siliziumkristallen bei hohen Temperaturen. Die aus Swirl-Daten gewonnenen Werte für die charakteristischen Eigenschaften von Zwischengitteratomen, d.h. ihre Bildungs- und Wanderungsenergie, fügen sich widerspruchslos in den durch andere Messungen erschlossenen Datensatz ein [4]. Dies gilt, falls angenommen wird, daß die Zwischengitteratome bei hohen Temperaturen im thermischen Gleichgewicht vorhanden waren. PETROFF und DE KOCK machten allerdings darauf aufmerksam, daß im Prinzip durch den speziellen Prozeß der Kristallzucht Zwischengitteratome auch im Nichtgleichgewicht eingebaut werden könnten, während die Gleichgewichtsfehlstelle (und damit auch die diffusionskontrollierende Fehlstelle) die Leerstelle sei [19]. Die Theorie eines solchen Prozesses kann zwar einerseits keine quantitative Aussage über die Konzentration der im Nichtgleichgewicht eingebauten Fehlstellenart machen, führt andererseits jedoch zu detaillierten Voraussagen über die relative Anzahl der eingebauten Fehlstellen in Abhängigkeit von Kristallzuchtparametern wie z.B. der Abkühlgeschwindigkeit. Die damit verbundenen Vorhersagen über Auftreten oder Nicht-Auftreten von Swirl-Defekten sind, wie in [11] ausführlich gezeigt wird, definitiv nicht erfüllt. Unserer Meinung nach ist damit eindeutig bewiesen, daß in Silizium bei hohen Temperaturen Zwischengitteratome die dominierenden atomaren Fehlstellen im thermischen Gleichgewicht sind. Gleichzeitig damit ist auch die Richtigkeit des SEEGERschen Zwischengitteratom-Diffusionsmodells bestätigt.
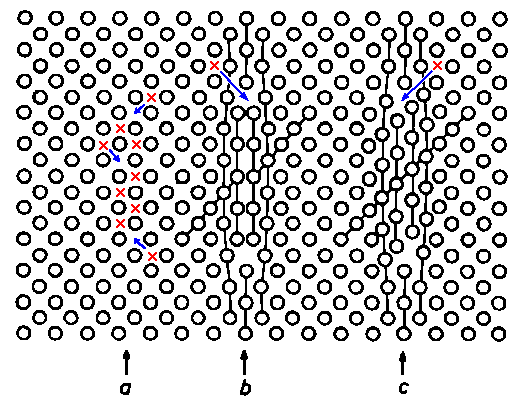
Fig. 9. Entstehung eines Versetzungsringes vom Zwischengitteratomtyp durch Agglomeration von Zwischengitteratomen
a) Zwischengitteratome (dargestellt durch Kreuze) kondensieren auf einer Netzebene des Kristalles. Diese Anordnung ist energetisch sehr ungünstig. – b) Durch Relaxation des Gitters bildet sich ein Versetzungsring mit Stapelfehler. – c) Der Stapelfehler wurde durch einen Scherprozeß (Verschiebung des Gitters in der Ringebene) beseitigt. Beide Arten von Versetzungsringen können durch weitere Anlagerung von Zwischengitteratomen wachsen
Das Endprodukt der Agglomeration von Zwischengitteratomen ist ein Versetzungsring vom Zwischengitteratomtyp, mit oder ohne Stapelfehler. Die zu Beginn der Agglomeration ablaufenden Prozesse, d.h. die Keimbildung der Versetzungsringe, sind jedoch sehr kompliziert und nicht so einfach, wie Fig. 9a es darstellt. In Silizium werden nämlich zur Bildung eines Versetzungsringes sehr große Keime benötigt, der Versetzungsring bildet sich deshalb über eine Zwischenstufe, den B-Defekt.
Bisher wurde auf die Natur der B-Defekte nicht eingegangen. In der Tat kann darüber auch nur spekuliert werden, da B-Defekte bislang noch keiner direkten, d.h. elektronenmikroskopischen Beobachtung zugänglich waren. Im Elektronenmikroskop wurde auch in Proben, in denen B-Defekte mit Sicherheit vorhanden waren (nachgewiesen z.B. durch Ätzung), nichts gefunden [15, 19]. Aus verschiedenen röntgenographischen und ätztechnischen Beobachtungen folgt jedoch indirekt, daß B-Defekte kleine, dreidimensionale und nahezu spannungsfreie Agglomerate von Zwischengitteratomen mit einem gewissen Gehalt an Kohlenstoff sind. Die Struktur dieser Agglomerate kann am besten durch das Modell eines Tröpfchens flüssigen Siliziums im Kristallgitter beschrieben werden. Da flüssiges Silizium eine etwa 10% höhere Dichte als kristallines Silizium besitzt, sind in einem solchen Tröpfchen mehr Atome als in einem gleichgroßen Volumen von kristallinem Silizium vorhanden. Ein Tröpfchen stellt also ein Zwischengitteratomagglomerat dar. Thermodynamiache Überlegungen zeigen, daß ein solches Gebilde bei hohen Temperaturen eine stabile Agglomeratform sein kann, vor allem, wenn im Tröpfchen Fremdatome gelöst sind [11]. Die hohe Selbstdiffusionsentropie von ca. 10 k zeigt, daß schon ein einzelnes Zwischengitteratom auf etwa 10 – 15 Atome „verschmiert" ist, d.h. selbst als ein sehr kleines Tröpfchen aufgefaßt werden kann. Die Agglomeration von verschmierten Zwischengitteratomen kann deshalb sehr wohl zu einem tröpfchenartigen Gebilde führen.
Mit sinkender Temperatur oder mit wachsender Größe wird ein Tröpfchen immer instabiler und wird schließlich in die stabile Agglomeratform eines Versetzungsringes umschnappen; es kann jedoch auch als Tröpfchen eingefroren werden. Um die im einzelnen ablaufenden Vorgänge zu verstehen, muß man einen Kristall mit einer gewissen Übersättigung an Zwischengitteratomen bei einer gegebenen Temperatur betrachten. Der Kristall kann diese Übersättigung beibehalten, d.h. die Zwischengitteratome bleiben dispers verteilt, er kann ein Tröpfchen bilden oder er bildet einen Versetzungsring. Welcher Prozeß abläuft, hängt von vielen Parametern ab, insbesondere von der Kohlenstoffkonzentration und von dem Kristalldurchmesser; letzteres wegen des Konkurrenzprozesses des Ausheilens der Zwischengitteratome an der Oberfläche. Für eine detaillierte Behandlung des Problems sei auf [11] verwiesen. Im folgenden werden nur die wichtigsten Ergebnisse dieser Betrachtung kurz dargestellt.
1) Mit sinkender Temperatur und damit wachsender Übersättigung an Zwischengitteratomen bildet sich ein tröpfchenähnliches Agglomerat, der B-Defekt. Die Keimbildung erfolgt heterogen an kleinsten Kohlenstoffausscheidungen. Stabilität und Wachstumskinetik des Tröpfchens werden durch den Einbau von Kohlenstoffatomen kontrolliert. Versetzungsringe können sich nicht direkt bilden, da dies bei hohen Temperaturen außerordentlich große kritische Keimgrößen erfordern würde.
2) Bei tieferen Temperaturen wird der B-Defekt instabil und wandelt sich u.U. in einen Versetzungsring um. Die kritische Temperatur für diese Umwandlung hängt von der Tröpfchengröße und damit von der Kohlenstoffkonzentration ab. Der frisch gebildete Versetzungsring wächst rasch, als einzige Senke in einem größeren Kristallgebiet zieht er auch Verunreinigungsatome, z.B. Sauerstoff, an sich. Die Entstehung der komplizierten Ringagglomerate läßt sich aus der Wechselwirkung zwischen diesen Verunreinigungsatomen mit dem ursprünglichen Versetzungsring verstehen.
3) Der Umwandlungsprozeß kann durch verschiedene Faktoren unterdrückt werden. Es wird dann ein B-Defekt eingefroren. Maßgeblich dafür ist vor allem die Abkühlgeschwindigkeit des Kristalles. Weiter zu berücksichtigen ist auch die Wechselwirkung zwischen frisch entstandenen Versetzungsringen und noch nicht umgewandelten B-Defekten in unmittelbarer Nähe.
Dieses noch spekulative Modell ist grundsätzlich in der Lage, die breite Fülle der verschiedenen experimentellen Beobachtungen an Swirl-Defekten (die hier nur sehr gestrafft wiedergegeben werden konnte) einheitlich zu erklären. Darüber hinaus bietet es Ansatzpunkte zum Verständnis einer Reihe von bislang unverstandenen Effekten, die unter dem Stichwort „prozeßinduzierte Defekte" bei der Herstellung von Halbleiterbauelementen immer mehr an Interesse gewinnen.
Die Untersuchung der Swirl-Defekte mit Hilfe der Hochspannungselektronenmikroskopie ergab, daß diese Defekte Agglomerate von Silizium-Eigenzwischengitteratomen sind. Dieses Ergebnis zeigt unmittelbar, daß in Silizium im thermischen Gleichgewicht bei hohen Temperaturen Zwischengitteratome die dominierenden atomaren Fehlstellen sind. Damit wurde die Theorie eines Zwischengitteratom-Diffusionsmechanismus bei hohen Temperaturen experimentell bestätigt. Die detaillierte Untersuchung des Agglomerationsprozesses ergab Hinweise für die Existenz dreidimensionaler Zwischengitteratom-Agglomerate in Silizium.
[1] A. SEEGER: Rad. Eff 8, 15 (1971).
[2] A. SEEGER und M. L. SWANSON: In „Lattice Defects in Semiconductors", Hrsg. R. R. HASIGUTI (University of Tokyo Press, Tokyo, und Pennsylvania State University, University Park and London) S. 93 (1968).
[3] A. SEEGER und K. P. CHIK: Phys. Stat. Sol. 29, 455 (1968).
[4] A. SEEGER, H. Föll und W. FRANK: In „Proc. 9th Int. Conf. Rad. Effects in Semiconductors", Dubrovnik 1976.
[5] W. C. DASH: J. Appl. Phys. 29, 736 (1958).
[6] T. S. PLASKETT: Trans. AIME 233, 809 (1965).
[7] E. SIRTL und A. Adler: Z. Metallkunde 52, 529 (1961).
[8] A. J. R. DE KOCK: Philips Res. Rept. Suppl. 1 (1973).
[9] A. J. R. DE KOCK, P. J. ROKSNOER und P. G. T. BOONEN: J. Cryst. Growth 22, 311 (1974).
[10] P. J. ROKSNOER, W. J. BARTELS und C. W. Bulle: J. Cryst. Growth 35, 245 (1976).
[11] H. FÖLL, U. GÖSELE und B. O. KOLBESEN: J. Cryst. Growth, im Druck.
[12] L. I. BERNEWITZ und K. R. MAYER: Phys. Stat. Sol. (a) 16, 579 (1973).
[13] B. O. KOLBESEN, K. R. MAYER und G. E. Schuh: J. Phys. E. (Scientific Instrum.) 8, 197 (1975).
[14] L. I. BERNEWITZ, B. O. KOLBESEN, K. R. MAYER und G. E. Schuh: Appl. Phys. Lett. 25, 531 (1975).
[15] H. FÖLL und B. O. KOLBESEN: Appl. Phys. 8, 310 (1975).
[16] D. M. MAHER und B. L. EYRE: Phil. Mag. 23, 409 (1971).
[17] H. Föll und M. WILKENS: Phys. Stat. Sol. (a) 31, 519 (1975).
[18] P. M. PETROFF und A. J. R. DE KOCK: J. Cryst. Growth 30, 117 (1975).
[19] P. M. PETROFF und A. J. R. DE KOCK: J. Cryst. Growth 35, 3 (1976).
Veröffentlicht in:"Jahrbuch der Akademie der Wissenschaften in Göttingen", HTML-Version 1/97
Verfasser:
H.
Föll und
B.
Kolbesen
Zurück zu Kapitel.1.3