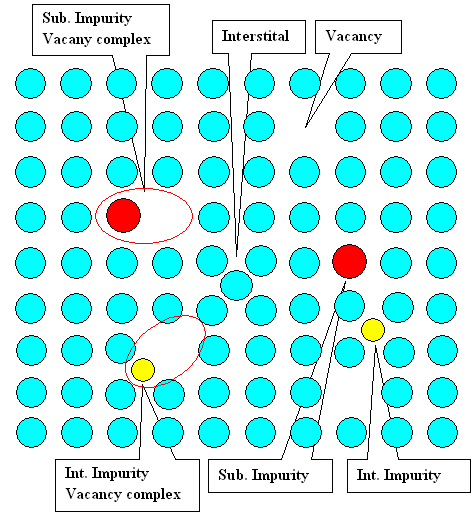
|
Consider a real crystal - take even a hyperpure
single crystalline Si crystal if you like. It's not perfect! It just is not. It will always contain some impurities.
If the impurity concentration is below the ppm level, then you will have ppb, or ppt or ppqt
(figure that out!), or... - it's just never going to
be zero. |
|
 |
The highest vacancy concentration your are going to have in simple metals close
to the melting point is around 10–4 = 100 ppm; in Si it will be far lower. On the other hand,
even in the best Si you will have some ppm of Oi (oxygen interstitials) and Ci(Carbon
substitutionals). |
|
 |
In other words - it is quite likely that besides your intrinsic equilibrium point defects (usually vacancies) squirming around in equilibrium concentration,
you also have comparable concentrations of various extrinsic non-equilibrium
point defects. So the question obviously is: what is going to happen between the vacancies and the "dirt"? How
do intrinsic and extrinsic point defects interact? |
 |
Let's look at the impurities first. Essentially, we are talking phase diagrams here. If you know the phase diagram, you know what happens
if you put increasing amounts of an impurity atom in your crystal. Turned around: If
you know what your impurity "does", you actually can construct a phase diagram. |
|
 |
However, using the word "impurity" instead of
"alloy" implies that we are talking about small
amounts of B in crystal A. |
 |
The decisive parameter is the solubility of the
impurity atom as a function of temperature. |
|
 |
In a first approximation, the equilibrium concentration of impurity atoms is given by the usual
Arrhenius
representation, akin to the case of vacancies or self-interstitials. This is often only a good approximation below
the eutectic temperature (if there is one). Instead of the formation energies and entropies, you resort to solubility energies and entropies . |
|
 |
There is a big difference with intrinsic point defects,
however. The concentration of impurity atoms in a given crystal is pretty much constant and not a quantity that can find
its equilibrium value. After all, you can neither easily form nor destroy impurity atoms contained in a crystal. |
|
 |
That means that thermal equilibrium is only obtained at one
specific temperature, if at all. For all other temperatures, impurity atoms are either undersaturated
or oversaturated. |
 |
Now the obvious: Vacancies, divacancies, interstitials etc. may interact with
impurity atoms to form complexes - provided that there is some attractive interaction. Interactions
may be elastic (e.g. the lattice deformation of a big impurity interstitial will attract vacancies) or electrostatic if
the point defects are charged. Schematically it may look like this: |
| |
|
|
 |
An impurity - vacancy complex (also known as Johnson
complex) is similar to a divacancy, just one of the partners is now an impurity atom. The
calculation of the equilibrium concentration
of impurity - vacancy complexes thus proceeds in analogy to the calculations for
double vacancies, but it is somewhat more involved. We obtain (for details
use the link). |
| |
| cC | = |
z · cF · cV(T)
1 – z
· cF | · exp |
D SC
k |
· exp |
HC
kT | | |
| | |
| | |
| | » |
z · cF · cV(T) |
· exp |
DSC
k |
· exp |
HC
kT |
|
|
|
 |
With cC = concentration of vacancy-impurity atom complexes, cF
= concentration of impurity atoms, cV = equilibrium concentration of (single) vacancies, and DSC or
HC = binding entropy or enthalpy, resp., of the pair. z , again,
is the coordination number. |
|
 |
That the coordination number z appears in the equation above is not surprising
- after all there are always z possibilities to form one complex. Note that the term 1 – z
· cF must be some correction factor, obviously accounting for the possible case of rather large
impurity concentrations cF. Why? - Well, for small cF, this term is just
about 1 and we get the approximation from above. |
|
 |
Note also that as far as equilibrium goes, we have a kind of mixed case here. The impurity
atoms have some concentration cF that is not an equilibrium
concentration. But if we redefine equilibrium as the state of crystal plus impurities (essentially we simply change the
G0 = Gibbs energy of the "perfect" crystal in one of our first
equations), than the concentration cC of vacancy-impurity atom complexes is an equilibrium
concentration. |
 |
The equation above for c C is quite
similar to what we had for the divacancy concentration. |
|
 |
If you forget the "correction factor" for a moment, we have identical exponential
terms describing the binding enthalpy, and pre-exponential factors of z · cV ·
cF for divacancies and z · cV · cV
for the vacancy - impurity complexes. |
|
 |
In both cases the concentrations decreases exponentially with temperature. However, assuming
identical binding enthalpies for the sake of the argument, in an Arrhenius plot the slope for divacancies would be twice
that of vacancy-impurity complexes - I sincerely hope that you can see why! |
 |
The total vacancy concentration c1V(total)
(= concentration of isolated vacancies + concentration of vacancies in the complexes) as opposed to the
equilibrium concentration without impurities c 1V(eq) is given by |
| |
|
|
 |
That's what equilbrium means! If impurity atoms snatch away some vacancies that the crystal
"made" in order to be in equilibrium, it just will make some more until equilibrium is restored. |
|
 |
cC thus can be seen as a correction term to the case of the perfect
(impurity free) crystal which describes the perturbation by impurities. This implies that cV >>
cC under normal circumstances. |
 |
We will find out if this is true and more about vacancy - impurity complexes in
an exercise. |
|
 |
You don't have to do it all yourself; but at least look at it - it's worth it. |
| |
|
| | |
|
|
© H. Föll (Defects - Script)