Debye-Huckel: The electrical potential of ions in solution

2.3.1 Debye-Hückel: The electrical potential of ions in solution

The starting point for the calculation is the Coulomb potential of ions in the solvent. For an isolated ion with charge \(z_i e\) in a medium of permittivity \(\epsilon\) at a distance \(r\) holds

\begin{equation*} \Phi_{ci} = \frac{z_i e}{4 \pi \epsilon r} = \frac{Z_i}{r} \quad \mbox{, with} \quad Z_i = \frac{z_i e}{4 \pi \epsilon} \label{def_Coulomb_pot} \quad. \end{equation*}

(2.20)

The ”ideal case” for a salt \(M_{\nu_+}X_{\nu_-}\) is that all ions have their actual position but without taking into account the Coulomb interaction. Thus the electrical work \(w_e\) is

\begin{equation*} w_e = G_m - G_m^{ideal} = \nu_+ (\mu_+ - \mu_+^{ideal}) + \nu_- (\mu_- - \mu_-^{ideal}) \label{def_we} \quad. \end{equation*}

(2.21)

From Eq. (2.10) we write

\begin{equation*} \mu_+ - \mu_+^{ideal} = \mu_- - \mu_-^{ideal} = RT \ln \gamma_\pm \quad, \end{equation*}

(2.22)

leading to

\begin{equation*} \ln \gamma_\pm = \frac{w_e}{\nu RT} \quad \mbox{, with} \quad \nu = \nu_+ + \nu_- \label{def_gamma_pm} \quad. \end{equation*}

(2.23)

This equation implies that we ”first” must find the final distribution of ions and then the work of charging them in that distribution. Since in turn the final distribution depends on the work of charging, this seems to be an impossible task. The standard way to solve such problems are self consistent solutions. For this we introduce a new parameter \(r_D\) (Debye length) and a modified Coulomb potential which takes explicitly into account the shielding effect of surrounding charges, i.e. the shielded Coulomb potential:

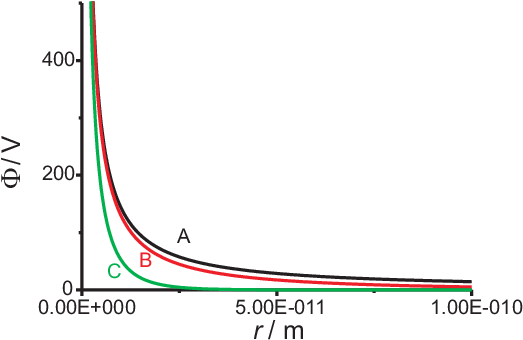
\begin{equation*} \Phi_{i} = \frac{Z_i}{r} e^{-r/r_D} \label{def_shielded_Coulomb_pot} \quad. \end{equation*}

(2.24)

Fig. 2.4 shows examples of this shielded electrical potential for different Debye length.

Figure 2.4: Shielded Coulomb potential for different Debye length’s \(r_D\). A: no shielding (\(r_D=\infty\)), B: low shielding (\(r_D=0.1\) nm), C: strong shielding (\(r_D=0.01\) nm)

The value of \(r_D\) is not known in advance but will be calculated ”self consistently”, i.e. to fulfill all relevant physical laws/restrictions. The self consistent solution is found from the Poisson equation which couples charge densities \(\rho\) to electrical potentials via

\begin{equation*} \Delta \Phi = -\frac{\rho}{\epsilon} \label{def_poisson_eq} \quad. \end{equation*}

(2.25)

Here \(\Delta\) is the laplacian which for spherical symmetry can be written as

\begin{equation*} \Delta = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} = \frac{1}{r^2}\frac{d}{dr} \left(r^2 \frac{d}{dr} \right) \label{def_laplacian} \quad. \end{equation*}

(2.26)

Combining Eq. (2.24) and Eq. (2.25) we finally get

\begin{equation*} \begin{split} - \frac{\rho_i}{\epsilon}& = \Delta \Phi_i = \frac{1}{r^2}\frac{d}{dr} \left(r^2 \frac{d\Phi_i}{dr} \right)\\ & = \frac{1}{r^2}\frac{d}{dr} \left(r^2 \frac{d}{dr}\left(\frac{Z_i}{r} e^{-r/r_D} \right) \right) = \frac{1}{r^2}\frac{d}{dr} \left(r^2 \left(-\frac{Z_i}{r^2} e^{-r/r_D} - \frac{Z_i}{r_D r} e^{-r/r_D} \right) \right) \\ & = \frac{1}{r^2} \left(\frac{Z_i}{r_D} e^{-r/r_D} - \left(\frac{Z_i}{r_D} e^{-r/r_D} - \frac{r \, Z_i}{r_D^2} e^{-r/r_D} \right) \right) = \frac{Z_i}{r \, r_D^2 } e^{-r/r_D} \quad, \end{split} \label{poisson_eq_1} \end{equation*}

(2.27)

i.e.

\begin{equation*} r_D^2 = - \frac{\epsilon \Phi_i(r)}{\rho_i(r)} \label{debye_Phi_rho} \quad. \end{equation*}

(2.28)

Still we have not solved our problem because we need a further equation relating the charge densities and (Coulomb) energies. For an ion with charge \(z_j e\) the energy within an electrical potential is given by

\begin{equation*} E(r) = z_j e \Phi_i(r) \label{def_E_Coulomb} \quad. \end{equation*}

(2.29)

Thus according to the Boltzmann distribution the ratio between the molar concentration \(c_j\) and the molar concentration in the bulk \(c_j^0\) (where the Coulomb energy is zero) is

\begin{equation*} \frac{c_j}{c_j^0} = \exp\left(\frac{-E}{kT}\right) = \exp\left(\frac{-z_j e \Phi_i}{kT}\right) \approx 1 - \frac{z_j e \Phi_i}{kT} \label{Boltzmann_E_Coulomb} \quad. \end{equation*}

(2.30)

The charge density \(\rho\) at a distance \(r\) from the ion \(i\) is the concentration of each type of ions multiplied by the charge per moles of ions

\begin{equation*} \begin{split} \rho_i & = N_A e \left(c_+ z_+ + c_- z_-\right) = F \left(c_+ z_+ + c_- z_-\right) \\ & = F c_+^0 z_+ \exp\left(\frac{-z_+ e \Phi_i}{kT}\right) + F c_-^0 z_- \exp\left(\frac{-z_- e \Phi_i}{kT}\right) \\ & \approx F c_+^0 z_+ + F c_-^0 z_- - \left(F c_+^0 z_+ \frac{z_+ e \Phi_i}{kT} + F c_-^0 z_- \frac{z_- e \Phi_i}{kT}\right) + ... \quad. \end{split} \label{Boltzmann_rho_Coulomb} \end{equation*}

(2.31)

Here we introduced the Faraday constant \(F = e N_A\). Due to overall charge neutrality \(F c_+^0 z_+ + F c_-^0 z_- = 0\). Using \(e = F / N_A\), \(N_A k = R\), and \(c\approx m \rho\) (\(\rho\): density of solution) we finally get

\begin{equation*} \rho_i = -\frac{ F^2 \Phi_i}{RT} \left( c_+^0 z_+^2 + c_-^0 z_-^2 \right) \approx -\frac{ F^2 \Phi_i}{RT} \left( m_+^0 z_+^2 + m_-^0 z_-^2 \right) \rho \label{rho_i_1} \quad. \end{equation*}

(2.32)

Introducing the ionic strength (cf. Eq. (2.18)) Eq. (2.32) can be rewritten as

\begin{equation*} \rho_i = -\frac{ F^2 \Phi_i}{RT} 2 I m^0 \rho \label{rho_i_2} \quad. \end{equation*}

(2.33)

Including this into Eq. (2.28) we get

\begin{equation*} r_D = \sqrt{\frac{\epsilon RT}{2 \rho F^2 I m^0}} \label{rho_i_3} \quad. \end{equation*}

(2.34)

So \(r_D\) decreases with increasing \(I\); thus \(r_D\) decreases with increasing concentration and charge of ions inside the ionic atmosphere (more shielding), and \(r_D\) increases with \(\epsilon\) and \(T\) (ionic atmosphere becomes more diffuse). The following table shows examples for Debye length’s for several concentration and charge numbers.


\(c\) [mol/l]	\(r_D\)(1-1) [nm]	\(r_D\)(1-2) [nm]	\(r_D\)(2-2) [nm]	\(r_D\)(1-3) [nm]

0.1	0.96	0.55	0.48	0.39

0.01	3.04	1.76	1.52	1.42

0.001	9.6	5.55	4.81	3.93

0.0001	30.4	17.6	15.2	12.4

To calculate the activity we have to calculate the electric work of charging the central ion when being surrounded by its atmosphere \(\Phi_{atmos}\). This is the potential difference between the total potential (cf. Eq. (2.24)) and the potential due to the central ion itself (i.e. the ideal case)

\begin{equation*} \Phi_{atmos}(r) = Z_i \left(\frac{e^{-r/r_D}}{r} - \frac{1}{r} \right) \label{def_Phi_atmos} \quad. \end{equation*}

(2.35)

The potential at the central ion (at \(r = 0\)) is obtained by taking the limit \(r \rightarrow 0\), i.e.

\begin{equation*} \Phi_{atmos}(0) = - \frac{Z_i}{r_D} = - \frac{q}{4 \pi \epsilon r_D} \label{def_Phi_atmos_0} \quad. \end{equation*}

(2.36)

Thus the potential of the ionic atmosphere is equivalent to the potential arising from a single charge of equivalent magnitude but opposite sign to that of the central ion and located at a distance \(r_D\) from the ion. The work of adding a charge \(dq\) to the central ion is

\begin{equation*} dw_e = \Phi_{atmos}(0) dq \quad. \end{equation*}

(2.37)

Thus the total molar work for fully charging the ion is

\begin{equation*} w_e = N_A \int_0^{z_i e} \Phi_{atmos}(0) dq = - \frac{N_A}{4 \pi \epsilon r_D} \int_0^{z_i e} q dq = - \frac{N_A z_i^2 e^2}{8 \pi \epsilon r_D} = - \frac{F^2 z_i^2}{8 \pi \epsilon r_D N_A} \quad. \end{equation*}

(2.38)

Using Eq. (2.23) we find

\begin{equation*} \ln (\gamma_\pm) = \frac{\nu_+w_{e+} + \nu_-w_{e-}}{\nu RT} = \frac{F^2 \left(\nu_+ z_+^2 + \nu_- z_-^2 \right)}{8 \pi \epsilon \nu r_D N_A R T} \quad. \end{equation*}

(2.39)

As already mentioned due to charge neutrality holds

\begin{equation*} \nu_+ z_+ + \nu_- z_- = 0 \label{c_neutr_1} \quad. \end{equation*}

(2.40)

Multiplying Eq. (2.40) with \(z_+\) we find

\begin{equation*} \nu_+ z_+^2 + \nu_- z_+ z_- = 0 \label{c_neutr_2} \quad. \end{equation*}

(2.41)

Multiplying Eq. (2.40) with \(z_-\) we find

\begin{equation*} \nu_+ z_+ z_- + \nu_- z_-^2 = 0 \label{c_neutr_3} \quad. \end{equation*}

(2.42)

Adding Eq. (2.41) and Eq. (2.42) we get

\begin{equation*} \nu_+ z_+^2 + \nu_- z_+ z_- + \nu_+ z_+ z_- + \nu_- z_-^2 = 0 \label{c_neutr_4} \quad, \end{equation*}

(2.43)

leading to

\begin{equation*} \nu_+ z_+^2 + \nu_- z_-^2 =- (\nu_+ + \nu_-) z_+ z_- = \nu \left|z_+ z_- \right| \label{c_neutr_5} \quad, \end{equation*}

(2.44)

and giving

\begin{equation*} \ln (\gamma_\pm) = - \frac{F^2 \left(\nu_+ z_+^2 + \nu_- z_-^2 \right)}{8 \pi \epsilon \nu r_D N_A R T} = - \frac{F^2 \left|z_+ z_-\right|}{8 \pi \epsilon r_D N_A R T} \quad. \end{equation*}

(2.45)

Including the definition for the final result for \(r_D\) of Eq. (2.34) we get

\begin{equation*} \log (\gamma_\pm) = - \left|z_+ z_-\right| \frac{F^3}{4 \pi \ln(10)} \sqrt{\frac{\rho m^0}{2 \epsilon^3 R^3 T^3}} \sqrt{I} = - \left|z_+ z_-\right| A \sqrt{I} \quad, \end{equation*}

(2.46)

which proves Eq. (2.17).

With frame

Debye-Huckel theory - activity coefficient of solutions