Figure 2.2:
a) Schematic drawing of the short range order of ions in a solution; b) Debye-Hückel limiting
case (red straight line) and the result of extended Debye Hückel theory
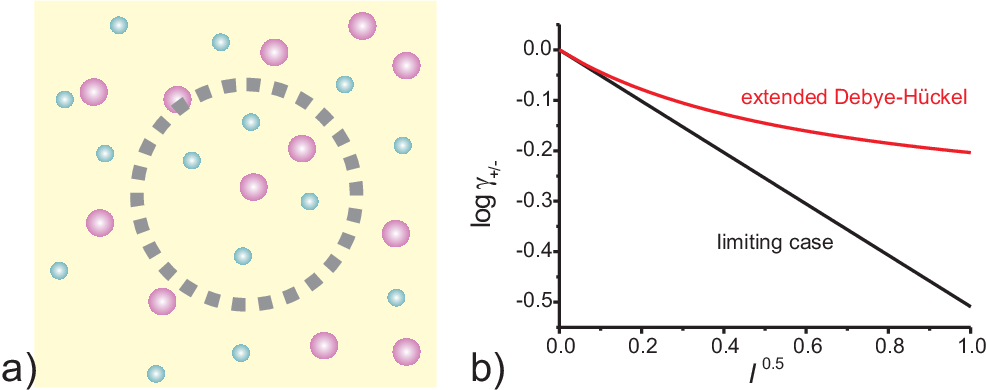
The long range and strength of the Coulomb interaction between ions typically dominates the non ideal behavior of ionic solutions. It is as well the reason that even for extremely diluted solutions these non idealities have to be taken into account. Opposite charges attract each other. Thus it is more likely that anions are found closely to cations, and vice versa. Although the over all solution is electrically neutral counter ions are on average more likely to be found close to any ion. This spherical haze of counter ions (ionic atmosphere) around a central ion has on (time) average the same charge but with opposite sign than the central ion, leading to a shielding of the central ion, as schematically shown in Fig. 2.2a).
The corresponding lowering of the energy is described by the difference to the ideal molar Gibbs energy, and thus is identical to \(RT \ln \gamma_\pm\). Before discussing the details we will just summarize the final results: At very low concentration the activity coefficient can be calculated from the Debye-Hückel limiting law
|
| \begin{equation*} \log \left( \gamma_\pm \right) = - \left|z_+ z_-\right| A \sqrt{I} \label{def_Debye_Huckel} \quad , \end{equation*} | (2.17) |
where \(z_+\) and \(z_-\) are the number of charged cations and anions, \(A\) is a constant (depending on temperature and solvent properties; e.g. \(A = 0.509\) for aqueous solution at 25\(^o\)C), and \(I\) is the dimensionless ionic strength, defined as
|
| \begin{equation*} I = \frac{1}{2} \sum_i z_i^2 \left(\frac{m_i}{m^0}\right) \label{def_ionic_strength} \quad. \end{equation*} | (2.18) |
As discussed in the following subsection and illustrated in Fig. 2.2 b) Eq. (2.17) holds for strong electrolytes, low concentration (up to \(10^{-2}\) mol/l), and low
charge numbers.
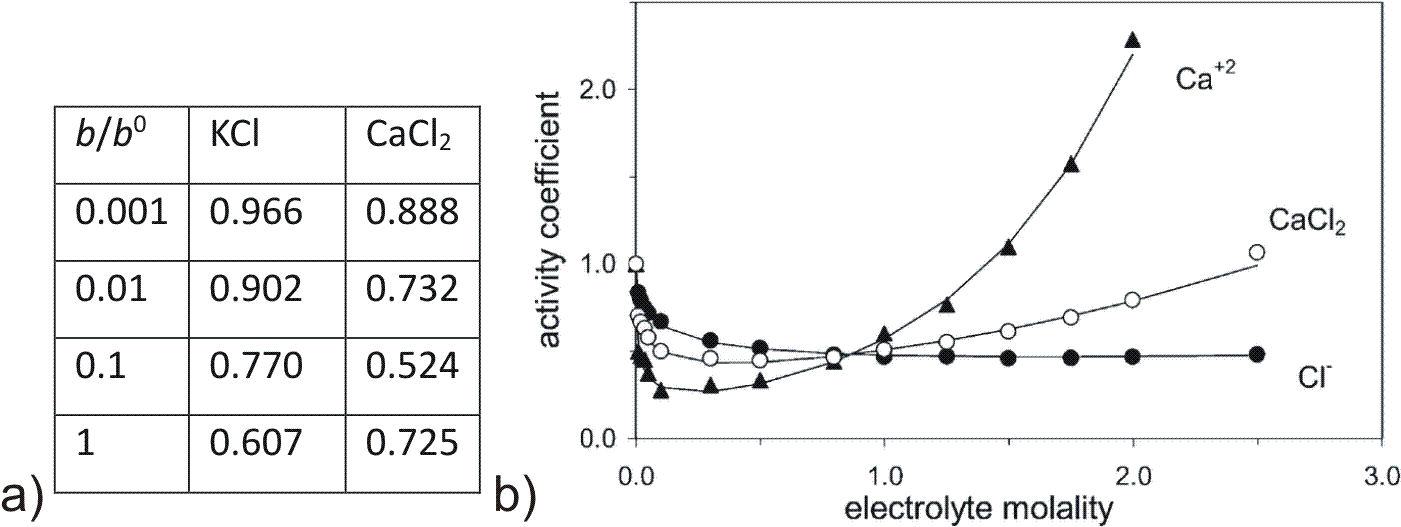
For higher concentration or ions with larger charge numbers as shown in Fig. 2.3 the extended Debye Hückel (or Davies) equation
can be used:
|
| \begin{equation*} \log \left( \gamma_\pm \right) = - \frac{\left|z_+ z_-\right| A \sqrt{I}}{1 + B \sqrt{I}} + C I \label{def_extended_Debye_Huckel} \quad . \end{equation*} | (2.19) |
Before going into any details some general aspects of the Debye Hückel approach are summarized
the classical Poisson equation (i.e. a differential equation) is solved which relates local charge densities \(\rho(r)\) to second derivatives of the electrical potential (energy)
the situation becomes ”difficult” because the local energy distribution \(E(r)\) in turn defines the charge distribution via the Boltzmann factor
instead of ”solving” the complicated differential equation a good guess for the charge density distribution (\(\propto \exp(-r/r_D)\) is chosen for which a self consistent solution for the Debye length \(r_D\) is calculated
the final results, i.e. the difference to the random distribution of charges without shielding is translated into an activity.
It is worth to go into all the tedious details of the solution because similar systems like the Debye layer at metal surfaces or the Helmholtz layers at solid electrolyte interfaces are solved in much the same way.
 |
 |
 |
 |
© J. Carstensen (TD Kin II)