Phase separation

5.9 Phase separation

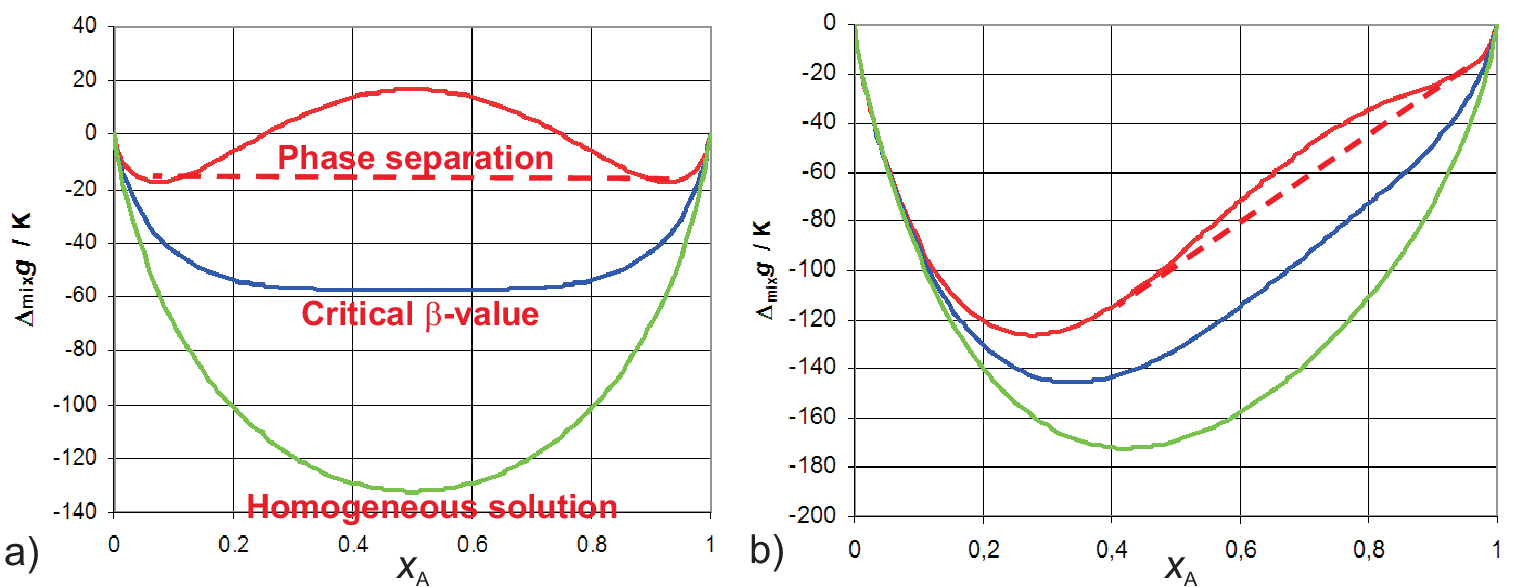
For the regular solution (cf. Eq. (5.26)) as well as for the asymmetric interaction enthalpy according to Eq. (5.28) graphs for \(\Delta_{mix} G_m\) for different values of \(\beta\) are shown in Fig. 5.6. For large values of \(\beta\) a concave branch in the molar excess Gibbs potential is found. Such parts are not stable (cannot exist) and must be replaced by a common tangent as illustrated by the dashed lines. Physically this implies a phase separation between the two compositions connected by the common tangent. For regular solutions the two connected points are arranged symmetrically around \(x_A = 0.5\) while for the asymmetric enthalpy both points are arranged asymmetrically.

Figure 5.6: Molar Gibbs potential for a) regular (symmetric) excess enthalpy and b) for an asymmetric excess enthalpy. Both show for large \(\beta\) values an unstable ( not strictly convex) regime leading to phase separation.

Next we will calculate for regular solutions the compositions between

Figure 5.7: The limits for phase separation vs. \(\beta\) for regular solutions (miscibility gap).

which phase separation exists. As visible in Fig. 5.6 these points are found at the minima of \(\Delta_{mix} G_m\), i.e.

\begin{equation*} \begin{split} 0 &=\;\; \frac{\partial \Delta_{mix} G_m}{\partial x_A} \\ &=\;\; R\,T\, \frac{x_A \ln x_A + (1-x_A) \ln (1- x_A) + \beta \, x_A \,(1-x_A) }{\partial x_A}\\ \Rightarrow & \quad 0 =\, \ln\frac{x_A}{1-x_A} + \beta \left(1 - 2 \,x_A \right) \\ \end{split} \label{eq:dG_ex_zero} \end{equation*}

(5.29)

This is a transcendental equation for which the solutions can only be found numerically. Fig. 5.7 shows the typical shape of the boundary curve vs. \(\beta\). As indicated above \(\beta \propto 1/T\) so with increasing \(T\) the dimensionless scaling factor \(\beta\) decreases. For \(\beta \lt 2\) phase separation does not exist anymore, i.e. it vanishes at high temperature. So \(\beta = 2\) is the critical value which is indicated in Fig. 5.6 a) as well. So phase separation exists only for repulsive forces A-B between the molecules. Phase separation is the response of the system to two opposing effects: the increase of entropy which always favors mixing and the increase of enthalpy due to the repulsive forces which supports demixing.