Excess functions

5.8 Excess functions

The concept of excess functions is similar to that of residual functions (cf. section 3.28), however, the excess functions are restricted to mixing. Both represent the difference between a real and an ideal state function. For the real as well as for the ideal system the sum of the separated pure components is subtracted to calculate the \(\Delta_{mix}\) parameter, i.e.

\begin{equation*} \begin{split} \Phi^{ex} &=\;\; \Delta_{mix}\Phi - \Delta_{mix}\Phi^{id}\\ & = \;\;\left(\Phi_{mixture} - \sum_i n_i \Phi^* \right) - \left(\Phi_{mixture}^{id} - \sum_i n_i \Phi^* \right) = \sum_i n_i \varphi_i - \sum_i n_i \Phi_i^* \end{split} \label{eq:Phi_ex} \end{equation*}

(5.25)

Excess functions typically follow specific restrictions, e.g. for regular solutions (solid solutions with random structure)

\begin{equation*} \begin{split} S^{ex} & =\;\; 0 \qquad \mbox{no excess entropy effects} \\ G^{ex} & =\;\; H^{ex} \neq 0 \qquad \mbox{excess energy/enthalpy contributions present} \\ \Delta_{mix} G_m & =\;\; \Delta_{mix} G_m^{id} + G_m^{ex} = \Delta_{mix} G_m^{id} + H_m^{ex} \quad \mbox{with}\quad H_m^{ex} = \beta \,R\,T\, x_A\,x_B = \Omega \, x_A\,x_B\\ \Rightarrow \Delta_{mix} G_m & =\;\; R\,T\,\left(x_A \ln x_A + x_B \ln x_B + \beta \, x_A\,x_B \right) \\ \end{split} \label{eq:S_ex_G_ex} \end{equation*}

(5.26)

Here \(\Omega\) describes the difference of the nearest-neighbor interaction energies between the molecules \(U_{A-A}\), \(U_{B-B}\), and \(U_{A-B}\). \(\beta = \Omega /( R\;T )\) is the corresponding dimensionless parameter which shows a strong temperature dependency:

\begin{equation*} \Omega = R\, T \beta \propto U_{A-B}-\frac{1}{2} \left( U_{A-A} + U_{B-B}\right) \quad \Rightarrow \quad \Omega = \beta = 0 \quad \mbox{for} \quad U_{A-B} \approx U_{A-A} \approx U_{B-B} \quad \mbox{(ideal solution)} \label{eq:beta_U} \end{equation*}

(5.27)

Link to caloric data:

\(\Omega, \,\beta \lt 0\): mixing is exothermic (heat release), \(\left|U_{A-B}\right| \gt \left|U_{A-A}\right|,\; \left|U_{B-B}\right|\), e.g. chloroform, acetone.
\(\Omega, \,\beta \gt 0\): mixing is endothermic (heat uptake), \(\left|U_{A-B}\right| \lt \left|U_{A-A}\right|,\; \left|U_{B-B}\right|\), e.g. aqueous solutions of hydrophobic compounds.
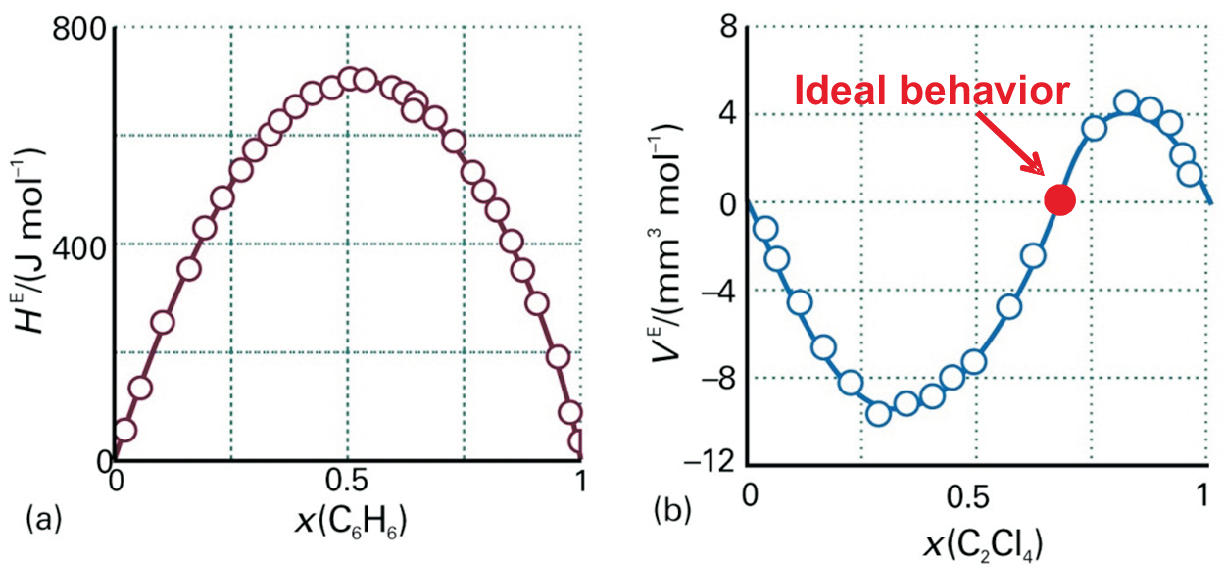
Normal regular solution: \(G^{ex} = H^{ex}\) are symmetric to \(x = 0.5\). An example for such a symmetric excess enthalpy is shown in Fig. 5.5 a) for mixing of tetrachloroethene and cyclopentane.
As an example for a non-regular solution the asymmetric excess volume for mixing of tetrachloroethene and cyclopentane is shown in Fig. 5.5 b).

Figure 5.5: Examples of excess functions. a) Excess enthalpy for mixing of benzene and cyclohexane (i.e. endothermic reaction); b) excess volume for mixing of tetrachloroethene and cyclopentane (i.e. contraction for small mole fraction and expansion for high mole fraction of tetrachloroethene).

Such an asymmetry as shown for the excess volume in Fig. 5.5 b) needs an asymmetric interaction between particles A and B which can mathematically be implemented for the excess enthalpy most easily as

\begin{equation*} \Delta_{mix} G_m = R\,T\,\left(x_A \ln x_A + x_B \ln x_B + \beta \, x_A^2 \,x_B \right) \quad \mbox{with}\quad H_m^{ex} = \beta \,R\,T\, x_A^2\,x_B = \Omega \, x_A^2\,x_B \label{eq:G_ex_asym} \end{equation*}

(5.28)