Figure 4.6:
a) Ehrenfest classification of 1\(^{\text{st}}\) and 2\(^{\text{nd}}\)
order phase transitions; b) \(T - C_p\) diagram illustrating a so-called \(\lambda\) transition.
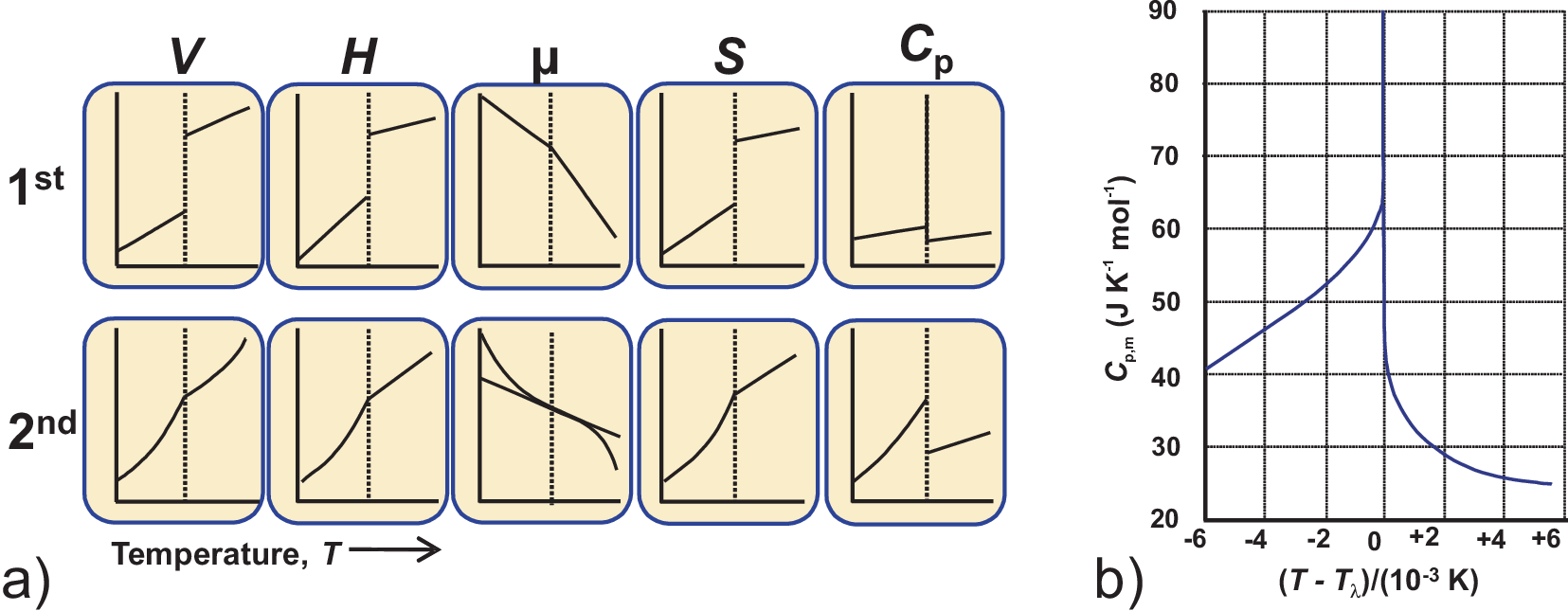
Phase transitions can be classified according to the type of change of state variables at the transition temperature as illustrated in Fig. 4.6 a). The first vaiant of this classification has been introduced by Ehrenfest:
For 1\(^{\text{st}}\) order transitions: the first derivative of the chemical potential \(\mu\) changes discontinuously. At \(T_{trans}\) the parameters \(V\), \(H\), and \(S\) change discontinuously, while \(C_p\) becomes infinite.
For 2\(^{\text{nd}}\) order: the second derivative of the chemical potential \(\mu\) changes discontinuously. At \(T_{trans}\) the parameters \(V\), \(H\), and \(S\) do not change discontinuously, while \(C_p\) remains finite and changes discontinuously.
The Ehrenfest classification is equivalent to a more modern classification:
First-order phase transitions involve latent heat. Latent heat is the heat released or absorbed by a chemical substance or a thermodynamic system during a change of state that occurs without a change in temperature.
Second-order transitions are continuous.
So the \(C_p\)-curves allow for an easy and rapid identification of the transition order. Fig. 4.6 a) shows a typical example for a so-called \(\lambda\) transition with an infinite \(C_p\) at the transition temperature.
There exist many practical/technically relevant aspects of 1\(^{\text{st}}\) order transitions in solids. First of all, they are simple to identify; due to the latent heat a clear peak is found e.g. in DSC and DTA. The technical relevance usually is related to the discontinuous and strong structural changes which solids exhibit at the transition. Frequently such strong structural changes can even lead to a splitting of the crystals. A typical example is the so-called tin pest, the transition from \(\alpha\)- to \(\beta\)-Sn. The related structural change is shown in Fig. 4.7. The degree of disorder is enhanced in the \(\beta\) phase, leading to a corresponding volume expansion and the splitting of the crystal.
 |
 |
 |
 |
© J. Carstensen (TD Kin I)
