Figure 4.3:
\(p-T\) diagram of CO\(_2\).
Sublimation and vaporization have much in common, mainly \(\Delta H_{sub,m}\) (\(= \Delta H_{melt,m} + \Delta H_{vap,m}\)) is larger than \(\Delta H_{vap,m}\).
|
| \begin{equation*} \frac{dp}{dT}=\frac{\Delta S_m}{\Delta V_m}=\frac{\Delta H_{sub,m}}{T\,\Delta V_{sub,m}} \label{eq:dpdT_Clapeyron_sub} \end{equation*} | (4.10) |
the sublimation line in the \(p-T\) diagram exhibits a larger slope. Repeating the calculation of Eq. (4.8) we find
|
| \begin{equation*} p_2 = p_1 \, \exp\left[ - \frac{\Delta H_{sub,m}}{R} \left(\frac{1}{T_2} - \frac{1}{T_1} \right) \right] \label{eq:Dp_dT_Clapeyron_sub} \end{equation*} | (4.11) |
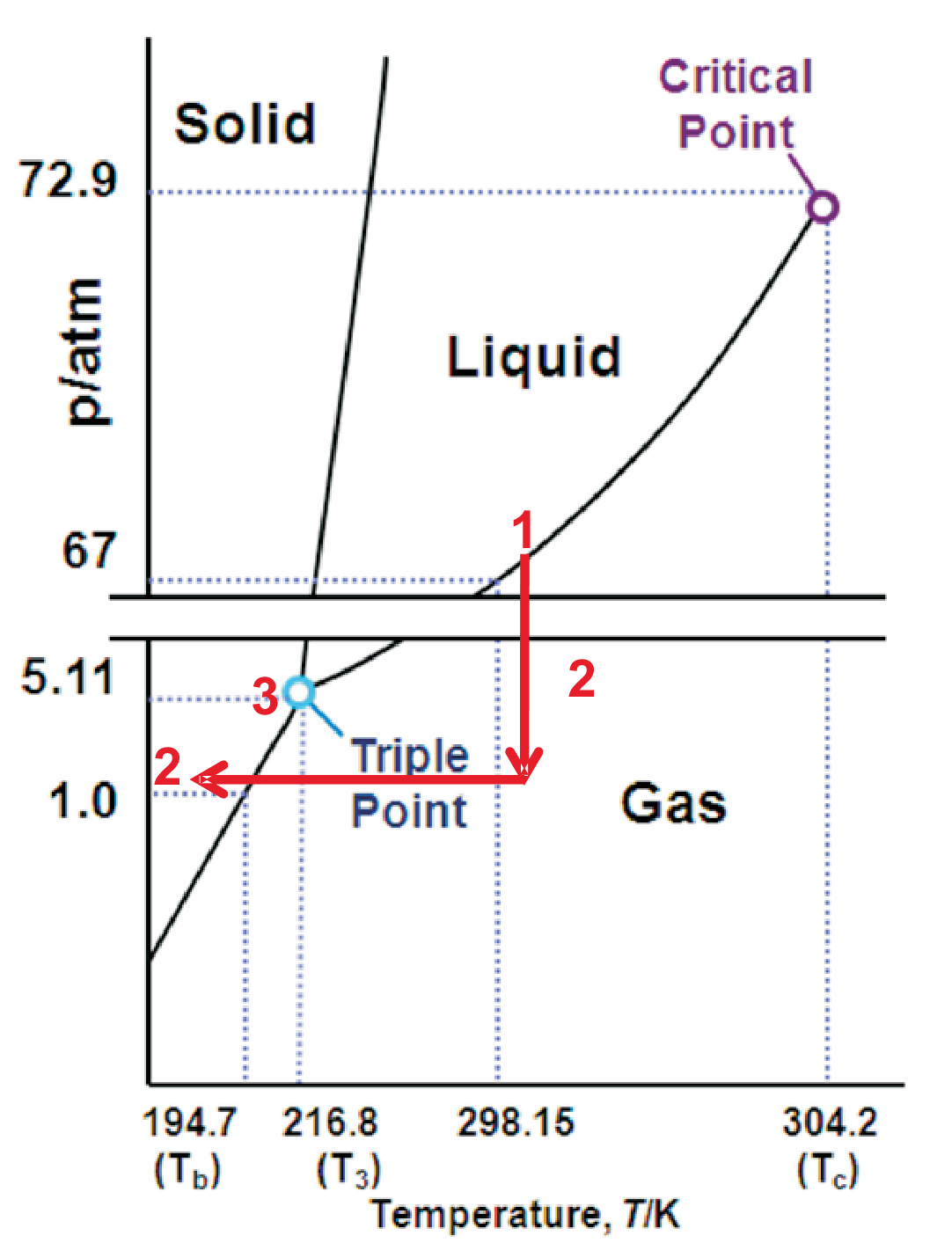
As an example the \(p-T\) diagram of CO\(_2\) is shown in Fig. 4.3. Since the sublimation curve is always steeper than
the vaporization curve an intersection between both curves is a must and a new phase line between solid and liquid is a
must as well. This explains the existence of a triple point.
Now we will use this phase diagram to
describe the sublimation of CO\(_2\) when opening a CO\(_2\) flask:
CO\(_2\) in a gas flask is under high pressure, hence it is in liquid and vapor state.
When releasing CO\(_2\) gas it cools by the Joule-Thompson effect thus forming solid CO\(_2\) which appears as snow-like dry ice by so-called de-sublimation.
The triple point at 5.11 atm (cf. Fig. 4.3) indicates sublimation of solid CO\(_2\) and not melting under atmospheric pressure.
 |
 |
 |
 |
© J. Carstensen (TD Kin I)