Examples for solid-solid equilibria

4.7.1 Examples for solid-solid equilibria

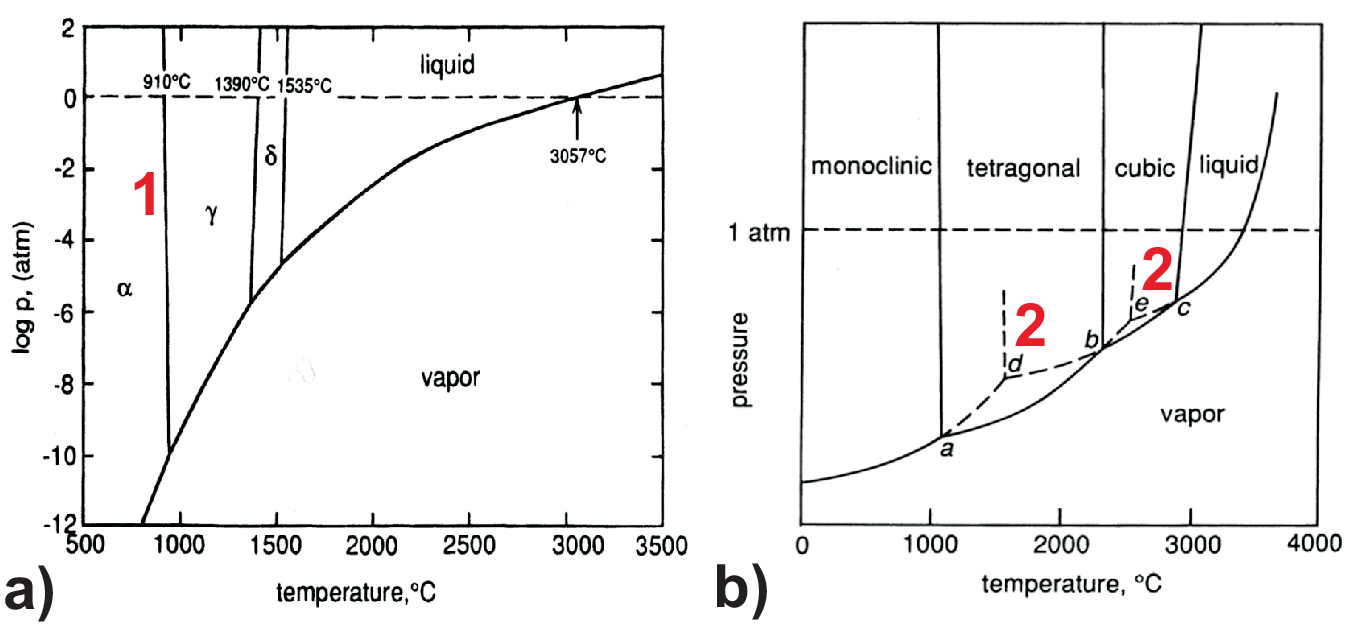
As further examples we will discuss phase diagrams of allotropes (elements) and polymorphs (compounds). These are elements (here Fe) and compounds (here ZrO\(_2\), zirconia) which can exist in more than one crystal form. Corresponding phase diagrams are shown in Fig. 4.4. In Fig. 4.4 a) the \(\alpha\), \(\gamma\), and \(\delta\) solid phase of Fe are shown. While the \(\gamma\) phase is (fcc) the \(\alpha\) and \(\delta\) phase are (bcc). The (fcc) phase has the highest packing density, thus the \(\gamma\) phase has the highest density and consequently the lowest molar volume. Therefore the \(\Delta V\) during transformation of \(\alpha\)-Fe is negative and according to the Clapeyron Eq. (4.5) implies the anomalous negative slope \(dp/dT\) of the phase boundary between the \(\alpha\) and the \(\gamma\) phase.

Figure 4.4: \(p-T\) diagrams: a) of Fe showing an anomalous slope of the phase boundary 1 between the \(\alpha\) and the \(\gamma\) phase; b) of ZrO\(_2\) showing two anomalous slopes and two metastable triple points at position 2.

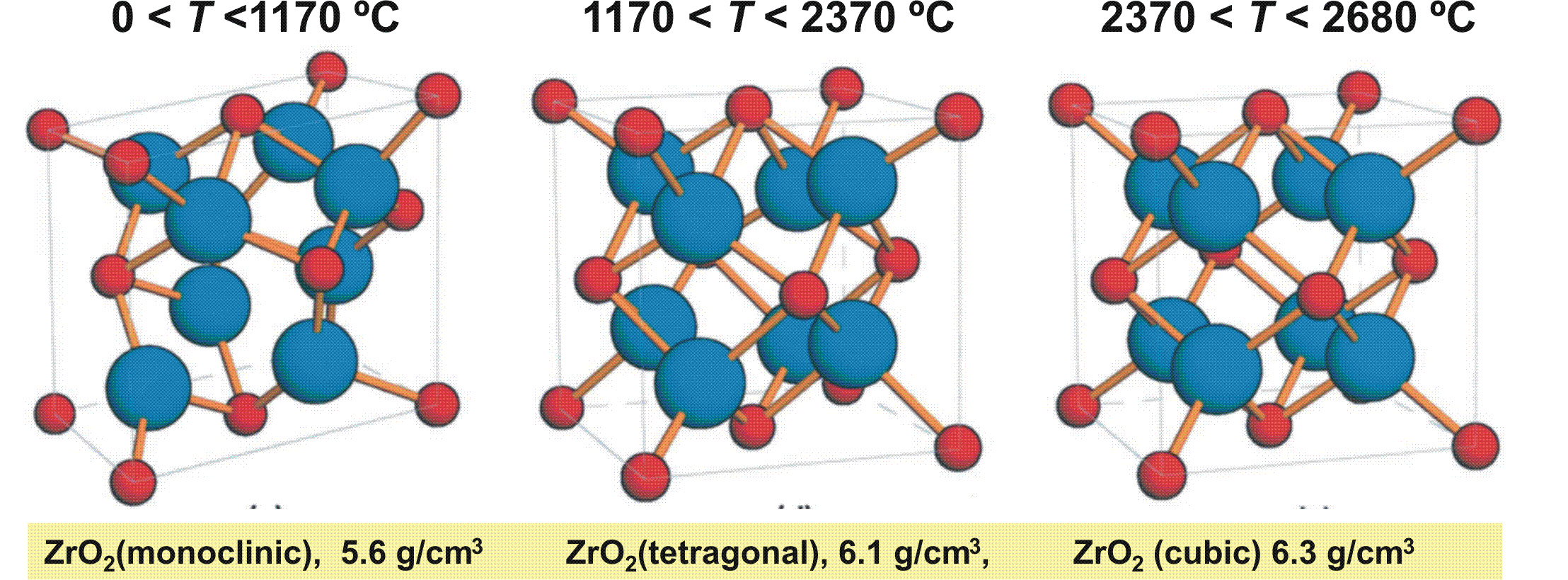
In the phase diagram of Fig. 4.4 b) for zirconia we see two anomalous slopes: one between the monoclinic and the tetragonal phase and one between the tetragonal and the cubic phase. The reason is related to the increase of point group symmetry from monoclinic to cubic which implies a density increase respectively volume reduction from the monoclinic via the tetragonal to the cubic phase (cf. Fig. 4.5). Such reorganization of crystal lattices needs time, i.e. is kinetically limited; so e.g. for fast changes of the temperature a different metastable behavior as indicated by the extrapolated dashed lines will be found leading to two metastable triple points, one at point d between vapor-monoclinic-cubic and a second metastable triple point at e between liquid-vapor-tetragonal. Waiting for thermodynamic equilibrium such metastable triple points are canceled out by the stable field where they are located in.

Figure 4.5: Crystal structure of zirconia showing a systematic density increase with increasing temperature which is an anomalous behavior.

With frame

Clapeyron’s equation and application to sublimation