Figure 1.5:
Maxwell construction for van der Walls isotherm for \(T' = 0.9\)
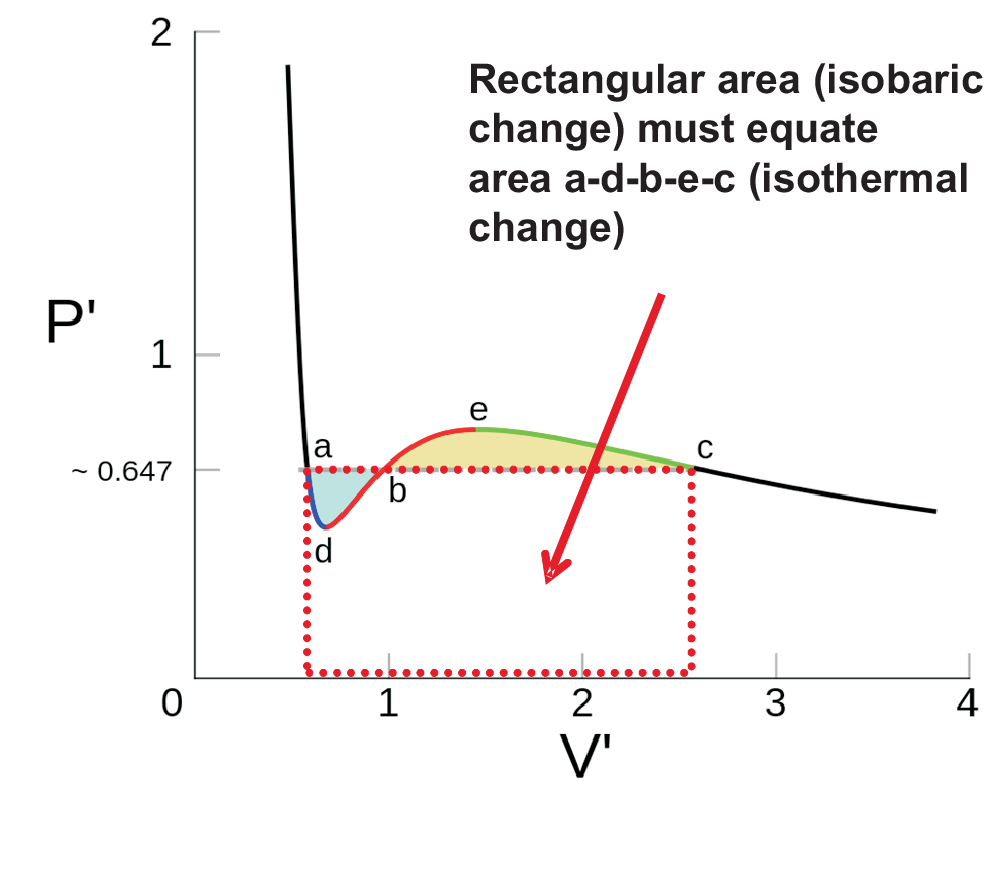
As shown in Fig. (1.5) the mathematical solution of the van der Waals gas equation shows two extrema while experimentally a straight line is found for slow volume changes, i.e. for changes representing thermodynamic equilibrium. For fast changes, i.e. non-equilibrium condition the features of subcritical isotherms represent
Metastable states, i.e. \((\partial p / \partial V)_T \lt 0\): a-d and e-c represent states of super-heated liquid and super-cooled vapor, respectively.
Unstable states, i.e. \((\partial p / \partial V)_T \gt 0\): d-e, defining the spinodal. This regime with positive slope is physically impossible, thus leading to spontaneous spinodal demixing.
For the two-phase regime the Maxwell construction replaces the isothermal loops by one isobaric straight line parallel to the \(V\)-axis for each isotherm so that equal areas are found for adb = bec.
The reversible expansion work performed by evaporating a liquid isothermally is represented by a STATE FUNCTION, the so-called Helmholtz free energy (\(F\)):
|
| \begin{equation*} w_{rev,p,T}=\Delta F = \int_{V_a}^{V_c} p dV \label{eq:wrev} \end{equation*} | (1.15) |
State functions are independent from the path of change. Thus isothermal and isobaric change
must give the same \(w_{rev}\). The isobaric change is represented by
a rectangle \(\Delta F(a \rightarrow c)\). The height of the rectangle is adjusted so that negative (a-d-b)
and positive (b-e-c) contributions of the isothermal loops cancel out. Thus \(F\) remains independent from
the path as demanded for state functions.
The van der Waals equation assumes a homogeneous single phase,
thus implying the inconsistencies and instabilities discussed above. The Maxwell construction implies two stable phases
with the composition of points a and c simultaneously existing in the system with varying volume fractions along the line
a \(\rightarrow\) c.
 |
 |
 |
 |
© J. Carstensen (TD Kin I)