Corresponding states (cs) and reduced variables

1.12 Corresponding states (cs) and reduced variables

In this section we will define a universal thermal equation of state matching for all compounds: \(f(p,V,T) = 0\). The basic idea is to find a representation for which the different intermolecular interactions of the different compounds can cancel out mathematically.
The strategy for the solution:

A special state (e.g. boiling point, critical point) represents a universal reference state for each substance which contains (all relevant) information about the intermolecular interactions.
Introduction of a ratio of two variables, ”reduced variables”:

\begin{equation*} \Gamma_r =\frac{\Gamma}{\Gamma_c} \label{eq:red_var} \end{equation*} (1.28)

Each of this reduced variables depends on the intermolecular interactions. Thus the intermolecular interactions (almost) cancel out.

As an example we will discuss the reduced form of the vdW equation.

\begin{equation*} p = \frac{R\, T}{V_m-b} - \frac{a}{V_m^2} \Rightarrow p_r p_c = \frac{R\, T_r T_c}{V_{m,r} V_{m,c}-b} - \frac{a}{(V_{m,r} V_{m,c})^2} \label{eq:vdW_red_var} \end{equation*}

(1.29)

Substituting

\begin{equation*} V_{m,c} = 3b \quad , \quad p_c = \frac{a}{27 \, b^2} \quad , \quad T_c = \frac{8 a}{27\, R\, b} \label{eq:vdW_red_var_set} \end{equation*}

(1.30)

we finally get the universal equation

\begin{equation*} p_r = \frac{8 T_r}{3 V_r-1}-\frac{3}{V_r^2} \label{eq:vdW_red_var_final} \end{equation*}

(1.31)

Although \(a\) and \(b\) are eliminated in the reduced form of the vdW equation they are still are present in form of the reduced variables.
For a later application we will need the isothermal compressibility \(\kappa\) which in the form of reduced variables is defined as

\begin{equation*} \kappa_{T}(V_r) = - \frac{1}{V_r} \left( \frac{\partial p_r}{\partial V_r} \right)^{-1} \quad \mbox{i.e.} \quad \kappa_{T}(1) = \left(-\frac{8\,T_r\,3}{\left(3\,V_r - 1\right)^2} + \frac{6}{V_r^3}\right)^{-1} = \frac{1}{6 \left(T_r -1 \right)} \label{eq:kappaT} \end{equation*}

(1.32)

Figure 1.6: Isotherms using reduced variables for several \(T_r\). Experimental data and theoretical curves.

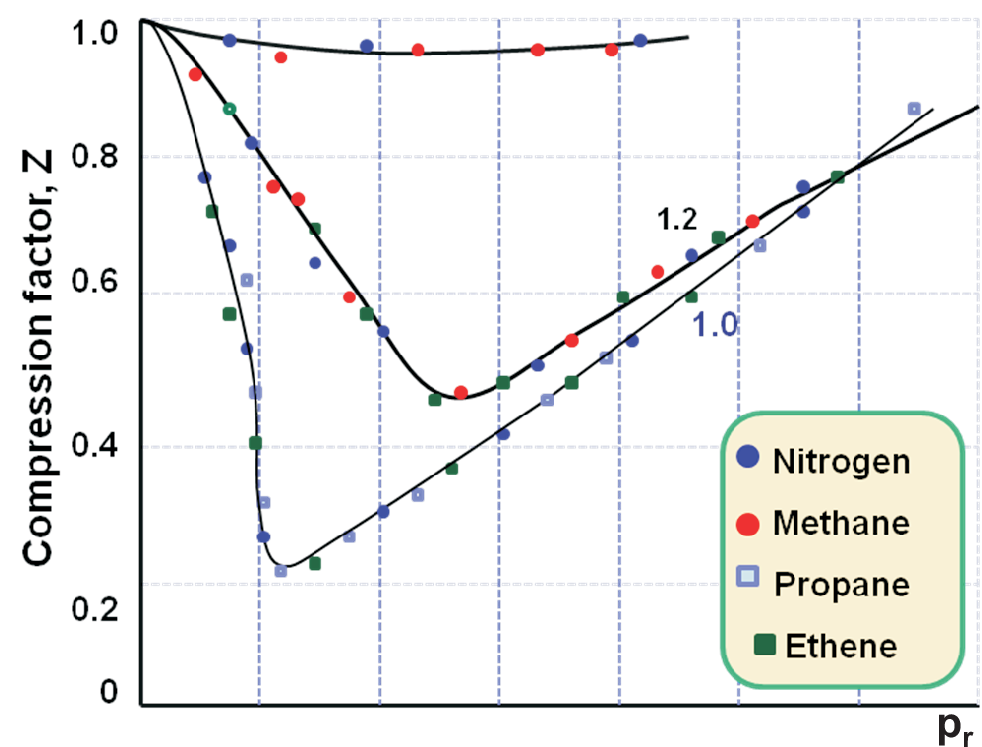
How well the concept of reduced variables and corresponding states can work is shown in Fig. 1.6.

Real gases at the same \(p_r\) and \(T_r\) exert the same \(V_r\) independent from their chemical nature, so \(f(p,V,T) \rightarrow f(p_r,V_r,T_r) = 0\).
One can adjust the conditions for each compound that the physical states of very different compounds are corresponding.
Strong deviations may be found for strongly anisotropic molecules: polar, non-spherical molecules (here correction terms available), and for H-bonding.
For \(T \lt T_c\) (i.e. \(T_r \lt 1\) not shown in diagram), the isotherms still show the vdW loops! Thus even the corresponding states do not solve all problems.