 |
It is important to look a bit more closely at the IV-characteristics
of a silicon pn-junction solar cell. The proper equation for that was
already introduced before |
|
 |
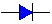
In a kind of short-hand notation, and because it is what electrical engineers
always do, we could symbolize that with the normal diode symbol: |
|
 |
|
 |
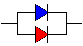
However, it is customary to use a "two diode"
model, where the first diode describes just the simple pn-junction behavior without carrirer generation and
recombination in the space charge region (SCR), and the second diode, which then must be switched in parallel, describes
the "non-ideality" of the real pn-junction. The equivalent circuit diagram then would consist of two diodes
in parallel: | |
 |
|
 |
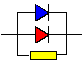
Since our junctions area is > 100 cm2, there might be regions where we
have a local "shunt" in the junction.
In the worst case this is a local short-circuit, caused for example because a metal
particle was embedded in the junction (we obviously need to be clean if we make those junctions). The best we can do to
model globally the many possibilties for shunts is to add a shunt
resistor
RSh in parallel to our diodes. "Global"
in contrast to "local" means that we only care for whatever
we can measure for the total solar cell, i.e. whatever we can get using only the two wires attached to it. |
|
 |
|
 |
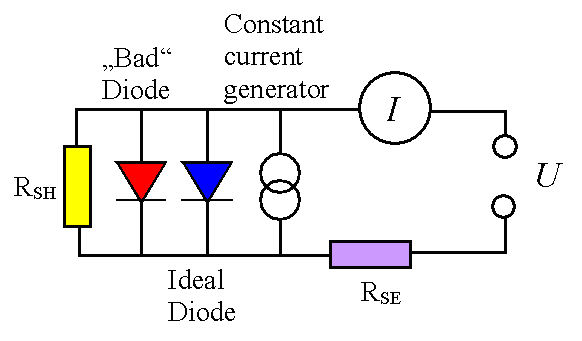
If we now add the internal series resistance
that is always there in series to what we already have, and consider that the photocurrent
flowing across the junctions(s) is simply a constant current generator
in electrical engineering terms, we obtain the final (and most simple) equivalent
cuircuit diagram of a solar cell and a somewhat modified master equation
for the equivalent circuit diagram: |
| |
 |
| I = |
I1 · |
æ
ç
è |
exp |
eUeff
kT |
– 1 |
ö
÷
ø |
+ |
I2 · |
æ
ç
è |
exp |
eUeff
nkT |
– 1 |
ö
÷
ø |
+ |
Ueff
RSH |
– IPh |
| "Ideal" Diode
| |
"Bad" Diode |
| |
| | |
| |
| |
|
| Ueff = |
U – I · RSE |
| |
| |
| |
|
|
 |
It is easy to see how the master equation was changed.
|
|
 |
First we switched from current densities j to currents I
and simply used the terms I1 and I2 as abbreviations for the pre-exponential
factors. I1 and I2 belong to the first (=ideal) and second (non-ideal)
diode in the equivalent circuit diagram. |
|
 |
Next, we considered that the junction voltage Ueff
is not identical to the externally measured voltage U but smaller by the voltage drop in the series resistor
RSE; i.e. Ueff=U – I
· RSE. |
|
 |
Then we generalized the non-ideal diode a bit by not just having a factor of two
in the denominator of the exponent, but an ideality factor n. For n=2 we would have the old
equation, but since we arrived at that part by rather hand-waving approximations, real (non-ideal) diodes may be better
described by some number other than 2. Our ideal diode has n=1. |
|
 |
Finally we add the current lost in the shunt resistor, which is given by Ueff
/ RSH. We have a positive sign because this current must be opposed to the photo current, which has
a negative sign in the conventions chosen. |
 |
Everything is quite clear - except that we can not solve this equation anymore
analytically and plot U(I) curves with RSH, RSE, and
n as parameters. |
|
 |
We have reached a point where we need to do some exercise: |
| |
|
 |
It is absolutely essential that you do this exercise - at least
ponder the question and look carefully at the solutions provided.
|
|
 |
You will learn that the series and shunt resistance does not only matter very
much but that we need to have extremely low values for the series resistance in the order of at most a few mW
per (10 × 10) cm2 solar cell. |
|
 |
Class Exercise:
Cu has a specific resistivity of about
2µWcm. Given a solid Cu wire with 1 mm2
cross section, what length will give you already 10 mW? |
 |
OK - coming back from the exercise (or just the solution) you learned that: |
|
 |
The series resistance
really matters for high efficiency cells; i.e. for all solar cells with let's say h > 10
%. In fact, optimizing the series resistance of a standard commercial solar cells (now, in 2007, with h
» 15 %) is one of the major tasks in solar cell R&D. We will look at some
number in another exercise coming up in the next module. |
|
 |
The shunt resistance,
if not extremely small, is less obnoxious for the efficieny h, but generates high leakage currents
in reverse direction, increasing with the voltage. This is deadly in modules
and thus cannot be tolerated either. |
|
 |
As far as the ideality factor is concerned, we do not notice major
problems. Here you have to look at details to see that the impact of the second diode is ther and detrimental. |
 |
The way to lump everything together globally
is to describe the global IV-characteristics with 3 numbers: |
| | |
| |
|
 |
1. The fill factor
FF,
defined as the relation between the area of the large yellow rectangle to the more orange area that is centered at the optimal working point.. That implies that the inner rectangle has the
largest area of any rectangle (Area =U · I= power delivered by the solar cell). The fill factor
measures the degree of "rectangularity" of the characteristics. |
|
|
|
 |
2. The open-circuit voltage
UOC,
i.e. the maximum voltage the solar cell will produce for the load resistor |
|
|
 |
3. The short-circuit current
ISC. |
|
|
 |
The efficiency
h then is directly proportional to UOC, ISC,
and FF, i.e. | |
| | |
|
|
|
| h | = |
const · UOC · ISC · FF |
|
| |
|
| |
| |
 |
How do we measure
the IV-characteristics of a real solar cell coming out of a production line? |
|
 |
Easy, you might think: Apply a voltage, measure the current, change the voltage,
measure the current again... Do it automatically by using a voltage ramp and keeping track of the current. Yes - that would
be perfectly OK except that solar cells from a real production come off the line at the rate of about 1
solar cell per second! Your measurement scheme is too slow for this because whenever the current changes the
capacity of the SCR must be recharged and this takes some time. |
|
 |
The way it is done is simple but powerful: You impress a constant current on your
solar cell by some external power source. At a given illumination intensity this takes a certain voltage as determined by
the IV-characteristics. If you change the illumination intensity, the voltage needed to drive the constant
current changes, too. If you change your illumination intensity very quickly be just using a flash light, your voltage can
follow just as quickly because you do not change the charge in the SCR capacitor. |
|
 |
The U(t) curve for a fixed current contains all the information
you want - but now you can get it with flashing speed! |
 |
You will actually do this in a Lab
course; the link provides the details. |
|
| |
|
Making Things Really Complicated |
| | |
 |
We are not yet done. Even if you have understood and committed to memory everything
pointed out above with all its implications, at least two topics must be still be addressed:
- How about other types of solar cells?
- Connection between local and global parameters.
|
 |
The first question can be dealt with rather easily - in principle:
|
|
 |
Whatever type of solar cell you have - Si bulk, µ-crystalline Si
thin film type, amorphous Si, CIGS or CdTe thin films, dye-based TiO2 electrolytic cells
- to name just a few, they must have some characteristics similar to a diode, and you can always find a suitable equivalent
circuit diagram for modelling its behaviour. |
|
 |
This equivalent circuit diagram might be somewhat different from the one given above, but
you always have the problems associated with series and shunt resitances after you solved the basic junction problems. |
|
 |
Quite often your choices for contacts are severely restricted and your series
resistances get so large that you only can get decent efficiencies by switching them in series in relatively small units.
More to that will be found in the link. |
 |
The second point is the difficult one. What he have discussed so far is the global
behaviour of a solar cell - what you measure for the whole "global" 100 mm x 100 mm cell, being uniformly
illuminated. |
|
 |
Now take your virtual knife and cut your solar cell into 10 000 (1 x 1) mm2
cells (without any damage and so on), an measure the IV-characteristics of those 10 000 local solar
cells. We assume that you know how to do this - it is possible albeit not easy. |
|
 |
If your global solar cell was not very uniform (rather likely for many solar cell types),
your local solar cells may show wildly different behaviour. The IV characteristics of the, let's say, 8
local cells that contain serious shunts (=short circuits) will be far more affected by this than your global cell (where
you have another 9 992 shunt-free cells switched in parallel). |
 |
You get the point: Your major global parameters
like short circuit current ISC, open circuit voltage UOC, fill factor
FF, series and shunt resistances RSE and RSH, diode ideality factor
n, are somehow determined by the local values, but it is not immediately
obvious how. |
|
 |
Besides the global short circuit current ISC,
which obviously is just the sum of the local
short circuit currents, for all other parameters the relationship between local and global parameters is non-trivial
or very complex. In the case of the global ideality factor n, the number
you extract from your global IV curves may not even have much to do with the junction properties. |
 |
Do we need to know the local parameters? After all, what counts is the real=global
solar cell. If it is as good as it should be, the local parameters might be of no interest. |
|
 |
Well - yes and no. Even if everything is OK globally, some small local defects may limit the
life time of the solar cell, i.e. be a risk to its expected 20+ years of harvesting energy. |
|
 |
More important, if you don't know your local parameters, you have very little guidance in
making your solar cell better. If, for example, the global short circuit current is
too low, that may indicate that it is just too low everywhere or that it might be allright on most parts of the cell but
really lousy in some small areas. If you don't know what is the reason, you can't fix the problem. |
 |
To give an idea what we are talking about, look at the pictures of the "multi-crystalline"
solar cell below: |
| |
|
 |
A perfect solar cell would show only one color - the optimal value. The colorful
pictures thus demonstrate that there is room for improvement and that you have to have the information contained in the
pictures to be able to make progress |
 |
How are maps like these obtained? With the so-called CELLO-Plus technique, developed
in Kiel. This is a rather sophisticated characterization technique that is described in some more detail in the link. |
© H. Föll (Semiconductor Technology - Script)


