Series and Parallel Connection

First Basic Question

We take a number N of solar cells; assuminng that all oft them are perfectly identical, to keep things simple at first. We also assume that there are no shunts in those solar cells, but that they have some series resistance RSE.
The first basic question now is : How can you deliver maximum power into some load resistor Rload - by switching the N solar cells in series or parallel?
Let's look at switching in parallel first.
Parallel connection of solar cells and power
Every individual solar cell delivers a current I, theses currents add up, and the current flowing through the load resistor Rload of the solar cell No. k under short circuit conditions is Iload(k) = k ·I
The corresponding total voltage drop in all N series resistor each with resistivity RSE is USE given by
USE  =  I · (RSE + 2RSE + 3RSE + .... + NRSE)
     
   =  I · RSE · ½N · N     (remember young Gauss?)
   
   =  I · RSE ·N2
2 
The product of maximum output voltage times current give some fictive power Pparallel akin to just multiplying ISC and UOC of the "ideal" solar cell. The actual power Pload, pdeposited into the load resistor depends, of course, on the value Rload; it will be maximal for some specific value of Rload but always smaller than Pparallel.
Pparallel   =  N · I · (Ucell – ½ N2 · I · RSE)
     
   =  N · I · Ucell  –  ½N3 · I2 · RSE
The total losses due to series resistors thus are at least Ploss, p = ½N3 · I2 · RSE
     
Now let's look at a series connection.  
Series connection of solar cells and power
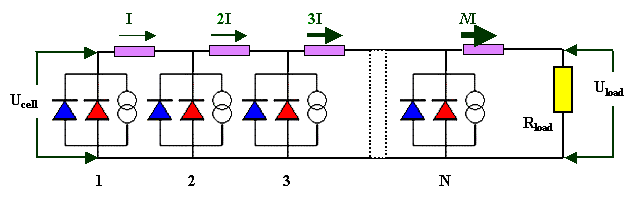
The current flowing through the load resistor is I  
The voltage Uload is N times the cell voltage minus the voltage drop in the internal resistance, i.e. minus N · RSE · I; we have Uload = N · (Ucell – I · RSe)  
The power Pseries deposited in the load resistor is such  
   
Pseries   =  I · N (Ucell – I · RSE)
     
   =  I · N · Ucell  –   I2 · N · RSE
 
   
Your total losses due to series resistors thus are Ploss, s = N · I2 · RSE  
   
The relation between the losses of a solar cell array in in parallel or in series thus are
 
Ploss, p 
Ploss, s  		 =  N3 · I2 · RSE
2 · N · I2 · RSE		  =  N2
2
 
In words: You must switch your solar cells in series! You loose far too much power if you have them in parallel
   

Second Basic Question

We take a number N of solar cells; assuminng that all oft them except for one are perfectly identical, to keep things not too simple anymore.
We consider two extrem cases for both variants, series and parallel connection of N – 1 identical good cells and one bad one:
  1. The bad cell has a very large series resistance and no noticeable shunt resistance
  2. The bad cell has a regular series resistance and a very small shunt resistance.
Let's see what will happen in the parallel world. All we have to do is to image that the series reistor of cell No. N is very large, or that the whole cell is just a small resistor in parallel to the load. What will happen?
In the first case you simply loose most of your voltage at the high series resistance of the defective cell. The power output will go down dramatically, or simply proportionally to the added series resistance. It will also matter which one of the N cells is the defective one.
In the second case you just add another parasitic load resistor to the intended load, funneling off some of the current. Again, the power output will go down dramatically, proportional to 1/RSH.
Let's see what will happen in the serial world.
In the first case you simply loose most of your voltage at the high series resistance of the defective cell, and it doesn't matter which cell it is. You can consider the surplus resistance as a parasitic addition to the load resistor. The power output will go down dramatically, again proportionally to the added series resistance.
In the second case you just loose the power not generated by the defective cell. The current of all the other cell passes through the (small) shunt resistance without much of a voltage drop.
Again, we have compelling reasons to go with series connections. We also see that we must watch out for high series resistance - it does more damage on the whole than the occasional shunt.
The most important insight, however, is that one bad cell in an array of, let's say 100 cells, may bring down the total efficieny of the module - that's essentially what we are discussing - quite disproportionally, i.e. not by just 1 %, but by far more.
     

Third Basic Question

We take a number N of solar cells; assuminng that all oft them are perfectly identical, but that one of them is completely shaded because a big leaf or a splash ot birds shit comßpletely covers it surface.
In other words: We take out the constant current generator of one cell.
What happens?
     
 
Ans so on. By now you get it.
 
 
Moduel technology is tricky
and needs attantion!
 

With frame With frame as PDF

go to 8.1.2 Solar Cell Current-Voltage Characteristics and Equivalent Circuit Diagram

© H. Föll (Semiconductor Technology - Script)