|
Next in importance to the elemental semiconductor Si, we have the III-V
compound semiconductors obtained by combining group III elements (essentially
Al, Ga, In) with group V elements (essentially N, P
, As, Sb). This gives us 12 possible combinations; the most important ones are probably GaAs,
InP GaP and GaN. |
|
 |
All of these III-V combinations crystallize either in the diamond lattice
like Si or Ge, often called "Zinc blende" or ZnS structure
(the term "sphalerite structure" is used, too), or in an hexagonal lattice known
as "wurtzite". For your edification both structures are shown and explained in the link. |
 |
What can III-V's do that Si cannot do? This is an absolutely essential
question for an engineer. |
|
 |
In your engineer mode (as opposed to your scientist mode)
you think exclusively in terms of applications and
products. |
|
 |
In a good first approximation, using a new material for an existing product is only
sensible if it makes the product better or cheaper
(or both). Looking at just "raw" Si single crystals, no other semiconductor comes even remotely close with
respect to prize / performance. There are simply no large practically defect-free cheap
wafers of other semiconductors! |
|
 |
So there must be a very compelling reason to use III-V's for application that Si
just can't hack. Obviously, this is optoelectronics for starters. |
|
 |
Obviously, because by now you know that Si has an indirect band gap and that means it will not emit light.
If we want to produce light emitting diodes (LED's'), we simply cannot use Si. |
 |
This brings us right to the most important set of III-V properties: Size
and nature of the band gap: |
|
 |
Class Exercise:
What would we like to have here? |
|
 |
Let's look at what we really have - if we like it or not: |
| |
| Properties |
Si | GaAs |
InP | GaP |
GaN |
In0,53Ga0,47As |
| Band gap [eV] |
1,12 | 1,42 |
1,35 | 2,26 | 3.39
| 0,75 | | Type |
Indirect | Direct |
Direct | Indirect |
Direct | Direct |
| Lattice | fcc |
fcc | fcc | fcc |
hex | fcc |
|
 |
Some questions should come up: |
|
 |
Where does that leave us with optics - what kind of light can
we get out of these compound semiconductors? The next figure will provide the answer for this question. |
|
 |
How about GaP? It has an indirect band gap but is still used for making LED's
(just believe it)?
Yes - there are tricks to get an indirect semiconductor to emit light. For some materials they work,
for others they don't. How it is done is beyond our ken at present; things like "excitons" (one of the many quasiparticles
of solid state quantum theory) "quantum wires" or "quantum dots" will be invoked. This link moves you on to a suitable module of a graduate course if you
are curious. |
|
 |
Does the last column imply that we can also have mixed cases? Yes - but only for thin films |
|
 |
Is it technically important if we have wurtzite or sphalerite; how about the lattice constants?
Yes and yes - this is even extremely important. |
| | |
|
Ternary and Quaternary III-V's |
| | |
 |
We have GaAs and GaP - what keeps us from mixing, forming for example GaAsxP1-x? |
|
 |
Nothing, of course - provided that the (ternary)
phase diagram provides for such a compound. |
|
 |
We can do even better by producing a quaternary
III-V compound with the structure IIIyIII1-yVxV1-x. |
 |
Now we have a large research program: Find out what can be done for all kinds
of combinations of III's, V's, x's and y's. |
 |
Fortunately we can make a few educated guesses of what might happen; and we do
that for ternary compounds (III-VxV1-x or IIIxIII1-vV)
to keep it easy. |
|
 |
Lattice constant: As
long as the lattice type doesn't change, the lattice constant most likely will just
smoothly change from one extreme value - e.g. GaAS - to the other - e.g. GaP. |
|
 |
Band gap: If we have no choice
but guessing, your best guess would be exactly as above: The band gap probably changes from one extreme value to the other
one - somehow |
|
 |
Direct - indirect band gap:
That's where guessing ends - except that for very small or very large x's we probably get whatever the pure
material will have. |
|
 |
Index of refraction:
Well - we will have a smooth change, most likely. |
 |
OK - we are now ready for a few diagrams |
| |
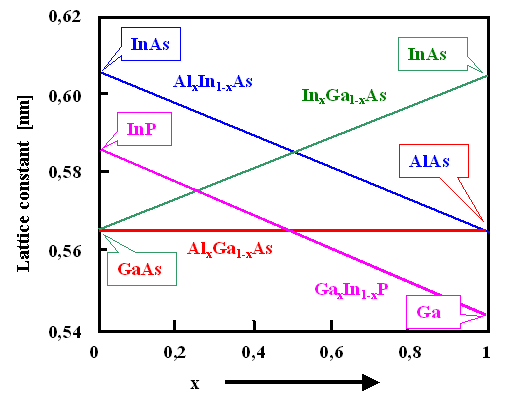
Lattice constant vs. composition for some ternary III-V's
|
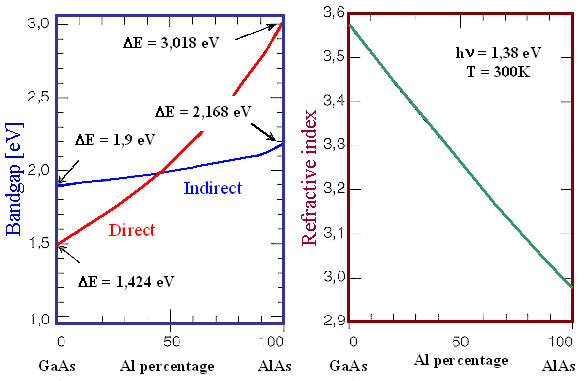
Band
gap and refractive index vs. composition for GaxAl1-xAs |
|
|
 |
So it is pretty much as expected. Pretty smooth changes of lattice constants and index of
refraction with composition, but not strictly linear with composition. Notice that the lattice constant hardly changes going
from GaAs to AlAs. This will have tremendous technical consequences. |
|
 |
The band gap case shows two curves - direct and indirect band gap for all compositions. Remember
that in wave vector (=k-space you might have all
kinds of band gaps and only the smallest one left after "adding up" is what we call "the" band gap.
In the picture above, the "direct" band gap "wins" for x < »
0,5; if you go more in the AlAs direction, it will be indirect. |
 |
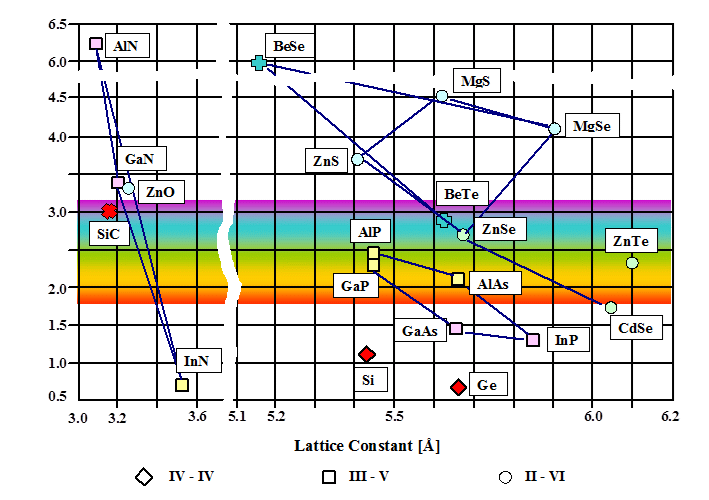
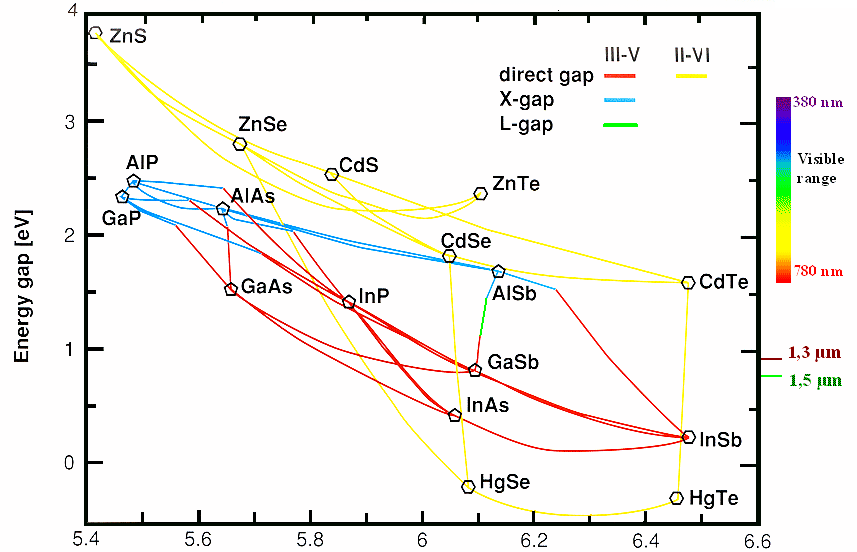
We are now ready for a first glimpse at the semiconductor "Master Graph": |
| |
|
|
 |
We see a large number of semiconductors in a band gap - lattice constant plot. We have two
plots because either one is a bit restricted. The spectrum of light is schematically superimposed, to give some idea about
the relation of the band gap energy to light color.
We also see a whole range of values for InN. The lower one
is probably the better one, as it turned out more recently. That tells us that even the most basic property of a semiconductor
material is not always ewasy to assess. |
|
 |
Lines connecting two semiconductors indicate that some mixture of the two is possible, and
how the lattice constant and the band gap will behave. For a HgTe - HgSe mixture, for example, the band gap would
decrease coming from both ends at first. However, the upper diagram does not have all possible lines drawn in. |
|
 |
Look at the GaAs - AsAl case in the lower diagram. You see that the lattice
constant does not change very much and that the band gap changes from direct (=red line) to indirect (=blue line) as soon
as you get AsAl "heavy". What we also see it that the common red LED is not
made from GaAs but from e.g. Ga0.7Al0.3As. |
 |
It looks like we have a great selection of semiconductors and their mixtures to
chose from. |
|
 |
Alas!
Choosing is one thing, making the semiconductor of your choice is something else. That's
were semiconductor technology comes in. |
|
 |
In reality, only a few of the many semiconductors shown in the Master Graph could be tamed
to perform by now. That's good news because it leaves something to do for you.
|
| | |
|
|
Optoelectronics - A Few Products |
| | |
 |
Optoelectronics is a formidable and strongly
growing field with many facets. Here we can only look at a few products in some arbitrary selection |
 |
Light emitting diodes
Where do
we find LED's now, and what is going to happen to the field? There is a long story to this question, we can only
look at some major points here. |
|
 |
We have LED's for all the little lights dotting every product that needs
electricity - TV's, dashboards
in cars, coffee makers, ... the list is rather long. There are two major and some minor technical requirement:
- Must be extremely cheap (< 1 € per LED); otherwise no mass market.
- Must last for many years because you cannot change or replace it.
- Should come in all colors (including infrared (IR)
for remote controls)
- Should have low power consumption.
- Should have defined angular dependence of emittance.
|
|
 |
The first two points are musts; the next three may be
negotiable.
For informations about the state of our coffee machine or TV we don't really need all colors. In fact, blue LED's
are a rather young achievement; they necessitate the mastering of GaN, which happens long after red LED's
were already ubiquitous.
Low power consumption is nice, but for the low intensity LED's it doesn't matter all that much. For some applications
you want to see that your machine is on from all angles - your LED thus should emit in all space angles; for some
other uses you want it more directed. |
|
 |
Then we have LED's replacing regular light bulbs, or at least the
light bulb in your flash light. In other words, they are competing against long established technology and must be cheaper
or better. What are the requirements?
Class Exercise:
Answer the question and compare your answer to the list above.
Class Exercise:
What is the state of the art? |
|
 |
Next we have special LED's, e.g. for infrared light.
Here is a link illustrating unexpected
uses of IR LED's right at the Institute of Materials Science in Kiel |
 |
So what do we need in terms of semiconductors and optoelectronics
technology? Let's start a list. |
|
|
- Band gaps in direct semiconductors with energies fitting all the photons or h·n
wanted - 0.5 eV - 4 eV would be fine, for example
- High efficiencies of operation, i.e. Power in (=U·I) / light power out should be close to 1
meaning 100 % efficiency.
- Absolute light power should be large ("100 Watt light bulb")
- White light should be possible.
- (Product) Lifetime is a concern.
|
 |
BNow let's look at more optoelectronic products. You do that: |
|
 |
Class Exercise:
Amend and discuss the list given so far. |
© H. Föll (Semiconductor Technology - Script)