 |
If you look at the basic model of a conjugated polymer chain with delocalized p
-bonds long enough, you must realize that you are simply looking at one possible embodiment of a one-dimensional free electron gas model. |
|  |
In a first approximation, we assume - as always - that the potential for the electrons along
the chain is constant, and that the chain has some length L - here we are. For the p
-electrons that we are looking at, we obtain the good old
free electron gas dispersion function |
| |
| Eelect = |
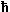 2 · k2 2 · k2
2 m |
|
|
 |
In a second
approximation, we now throw in some periodic potential and consider the Fermi energy.
|
|
 |
This gives us Brillouin zones, changes of the dispersion function mostly on Brillouin zone
boundaries, and some wave vector kF separating occupied from unoccupied states. The dispersion
function shown just above will change to something more complicated with a band gap at the Brillouin zone boundaries. |
|
 |
Notice that the emphasize here is on some
periodic potential. The whole apparatus mentioned above works for any periodic potential,
not just for a periodic array of atoms or ions. |
 |
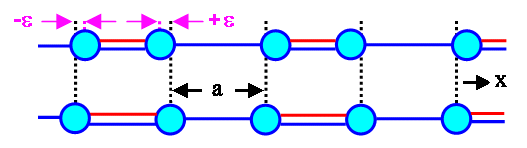
In particular, a periodic distortion of the bond lengths
as shown below must be expected to somehow influence the behavior of the electrons in the systems - we may consider it to
be a periodic potential, too. |
|
 |
The picture below shows a possible elastic deformation - we shortened the double bonds by having some strain
2e, or alternatively, we elongated the single bonds by 2e |
| |
|
|
 |
This does not happen, because the double bond has an intrinsically,
i.e. electronically determined shorter bond length, but only because we - in this thought experiment - put some elastic
stress on the bonds. |
 |
We now have some elastic or mechanical energy E mech
stored in the strained bonds. The magnitude of Emech for one unit volume of the chain is simply |
|
|
| Emech(e) |
= |
s · e
2 | = |
Y · 2e2
2
| = |
Y · e2 |
|
|
|
 |
We substituted the stress s via s = Y
· e with Y = Youngs modulus. |
|  |
If you have some doubts about this formula - that's fine. But we only want to get the flavor of what is
happening, and in principle what we are doing is correct, give or take some factor of 2 or so. |
 |
Now, after we "somehow" mechanically deformed the chain in a periodic fashion, we
consider the effect on the p-electrons. |
|
 |
Without the deformation, they experience a constant potential U = 0 - that was, after all,
our starting point within the free electron gas model. |
|
 |
But with the deformation, they now see a periodically changing potential U(e).
We changed the positions of the atoms or ions, and the only effect that can have is to induce a periodic variation of the
potential energy for the electrons which will depend on e, of course. |
|
 |
We have no idea how large that effect is going to be, but the most simple formula we can use in a first
approximation would be |
| |
| U(e) = |
2 · A · e · cos |
æ
ç
è |
p
a |
· x |
ö
÷
ø |
|
|
|
 |
The proportionality constant A
is actually of considerable interest in general terms: It can be interpreted as some kind of coupling constant between
electrons and phonons . |
|  |
After all, a periodic displacement of atoms from their regular lattice positions is a phonon - even if doesn't bounce around a crystal. |
 |
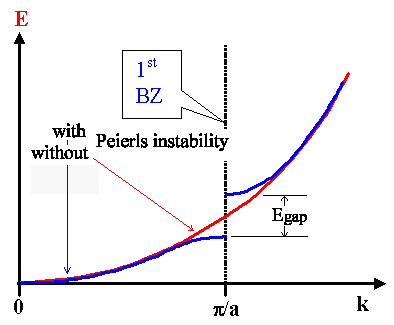
Now let's look at what all that means in reciprocal space. We can use one of our old pictures for this in slightly modified form |
| |
|
 |
We have a band gap at the Brillouin zones, of course. It's magnitude is directly given by the
amplitude of the periodic potential, i.e. we have |
| |
|
|
 |
The last thing we need to notice is that the available states will be occupied right up to
the 1st Brillouin zone, because we have one "free" electron per lattice constant. |
 |
What we see now is that the total energy of the "free" electrons is smaller if there
is a band gap. But we don't get it for free - we have to pay some elastic energy Emech
to get a reduction in the electronic energy. |
|
 |
In order to find out out if "pays" to invest some elastic energy Emech
with respect top the return of electronic energy, we have to look eat the total energy Etotal (e) = Emech(e) + E elec(
e) and see if it has a minimum , and if yes, for what kind of elastic deformation . |
|  |
Doing that is not exactly easy - even for our rather simple minded approximations used so
far. |
|
 |
But it is not so difficult either, so that we cannot understand the gist of the argumentation
here |
 |
So let's not go onto details, but just discuss what needs to be done. |
|  |
First, we need some formula for the dispersion curve for the case with a band gap. Whatever
this formula will be, it depends on the magnitude of the band gap, i.e. on the amount of strain e
and on the constant A , which describes how much an elastic deformation influences electrons. |
|
 |
This formula, as always, also defines the available states for the electrons in k-space.
|
|
 |
The total electronic energy of the system then is simply the integral over this curve up to
the last occupied states, i.e. up to the Fermi wave vector or Fermi energy. |
|
 |
To this integral we add the elastic energy that we have to
invest to produce the periodic potential in the first place. This gives us the total energy |
| |
|
Etotal(e) = Eelec(e) + Emech(e) |
|
|
|
 |
Then we find the minimum of that total energy by differentiating it with respect to the strain
e and setting the resulting differential quotient to zero, i.e. we do |
| |
¶
Etotal(e )
¶e |
= |
¶
¶e |
æ
ç
è |
kF
ó
õ
0 |
E(k,e, A ) + Y · e2 |
ö
÷
ø |
= 0 |
|
|
 |
This will be our master equation. It looks pretty formidable even for the most simple model
and approximation we can chose. We can easily make it more complicated by looking at more sophisticated models, but it always
will have always one basic property: It either has a solution or it doesn't.
|
|
 |
If it has a solution, it means that a Peierls instability does occur because it is energetically
favorable. An inherent symmetry will be broken by some elastic deformation, and a band gap in electronic states will open
up. This gap might be so small that at room temperature it will not be noticed, but it will be there nonetheless. |
|
 |
If it does not have a solution, it means that there is
no Peierls instability - bond lengths are the same, the band structure does not have a gap, and the (model) material is
a conductor. |
 |
As it turns out, for out problem the master equation does have a solution, and that is also
true if you use more sophisticated models or math. |
|
 |
In the most simple form, one obtains for the strain e that
minimizes the total energy something like |
| |
| e |
= |
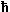 2 · kF2 2 · kF2
m · A | · |
1
sinh – (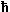 2 · kF · p
· Y / 4 · m · A2) 2 · kF · p
· Y / 4 · m · A2) |
|
|
 |
It's not so obvious, what this means. Look up the hyperbolic sinus here
if you are unsure what it looks like . |
|
 |
Playing around with numbers a bit (which means making some educated guesses about
the range of possible values for A), one realizes that the argument of the hyperbolic sinus tends to be >>1,
which means we can approximate the equation from above by |
|
|
| e |
» |
2 · 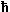 2 · kF2 2 · kF2
m · A | · exp – |
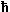 2 · kF · p · Y 2 · kF · p · Y
4 · m · A2 |
|
|
|
 |
That is an interesting equation, because it comes up in similar form for various
problems, most noteworthy, perhaps, for superconductivity
, which also owns its existence to some kind of Peierls instability |
 |
Looking back, we now can draw some more conclusions: |
|
 |
For conjugated carbon chains, the Peierls instability has a large effect. For
the most simple real conjugated polymer which is poly ..... , it causes the transition from a one-dimensional metal to a
semiconductor with a rather large band gap of » 1.6 eV. |
|
 |
But any periodic arrangement of atoms, ions
or whatever, might undergo some kind of Peierls instability. It might be so small, however, that it is not noticeable at
finite temperatures. |
|
 |
The effect is not limited to one-dimensional
chains. As long as we can consider the x-, y- and z-dimension of the electronic
energy separately, as we do in the free electron gas model, we will have a Peierls instability in three dimensions, too.
|
 |
However, let's not get too general at this point. The Peierls instability results from the
coupling of phonons and electrons, and this is but a first step into a complicated world of collective phenomae in solids. |
|
 |
It may happen, and if energetically favorable, it will happen, causing
large effects on occasion, as for conjugated polymer chains. But other effects might happen, too, and it would be too simple
minded to invoke the Peierls instability for everything out there not yet understood by us. |
| | |
© H. Föll (Semiconductors - Script)
![]() Vocabulary for Semiconducting Polymers
Vocabulary for Semiconducting Polymers