|
Essentially, edge-emitting LEDs
will almost automatically work as lasers, too, if simple conditions are met |
|
 |
The active region must end in "mirror" surfaces,
which are most simply obtained by cleaving
the crystal. Diamond and zinc-blende type crystals will always cleave along {110} planes, which contains the fewest
bonds (that's how diamonds are processed, anyway). The cleavage planes are often almost atomically flat. |
|
 |
Than parts of the light will always be reflected back and the ends of the crystal act as
a Fabry–Perot resonator. The reflectance R (for nair = 1) is given by |
|
|
| R | = |
æ
ç
è |
nsemi – 1
nsemi + 1
| ö
÷
ø |
2 |
|
|
|
 |
With nsemi = index of refraction of the semiconductor »
3.6, we have R = 0.32, i.e. almost a third of the light is reflected back into the active zone. |
|
 |
Theoretically, we also should have the total length of the active
zone to be a multiple of the wave length desired. However, since the total length is much larger than the wave
length, some wave length will always "fit" and lasing will occur as soon as the gain is large enough to compensate
the losses. |
 |
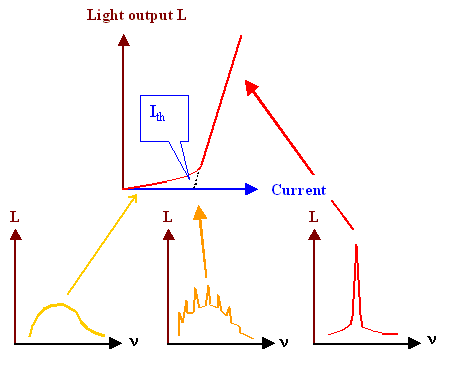
We will have a rather poor laser. Nevertheless, it will show the general behavior
of semiconductor lasers as illustrated below: |
|
|
|
|
 |
For currents below some threshold current Ith, the device will be
a simple LED emitting light with a rather wide frequency distribution. |
|
 |
As soon as enough carriers are injected to cause sufficient inversion, some modes of the resonator with the "right" wavelengths will become amplified
and appear as small peaks on the spectral distribution of the light. |
|
 |
Well above threshold, the frequency with the highest coefficient "wins" and the
laser might emit only one wavelength. |
 |
In order to have high efficiency and a single
mode, we must maximize the density of photons [i.e., u(n)] and
the gain coefficient [g (n)] in the same
active area of the device. |
|
 |
This is not a condition automatically met
– quite the opposite. The gain coefficient is mostly a function of the positions of the quasi Fermi energies, i.e.,
the electron densities. While the laser is in operation, it is essentially a function of the carrier injections across some
junction. We cannot expect that this is homogeneous everywhere in the active region; g is thus a function
of (x,y,z), too. |
|
 |
Light is reflected, diffracted, and absorbed according to the (complex)
refractive index
nr of the medium. This is foremost a function of the material itself, but also of the densities
of available electrons. In regions with a high gain coefficient we have a high density of electrons, too, and thus a changed
index of refraction. |
|
 |
If, in a thought experiment, we would keep the semiconductor at equilibrium (no currents,
no inversion) and feed the light into the resonator from the outside, u(n) would
be a function of the refractive index only. However, since we absorb and produce light by high densities of electrons in
non-equilibrium, we change the optical properties of the resonator and u(n) couples
to g( n) – we have rather complex conditions not amenable to simple analysis. |
 |
Still, we have two basic options looking at
the extremes: We can define the active area – or better, volume – by large values of u(n)
or
g(n) – irrespective of what the other quantity does. |
|
 |
If we choose u(n), all we have to do is to surround
the active volume by "mirrors" on all 6 sides, a feat that can be achieved by enclosing the active volume
with material that has a lower index of refraction. At the same time we make sure that in the active volume – and
possibly around it – we have a large gain coefficient by injecting carriers all over the place. |
|
 |
If we choose g(n) for the definition of the active
volume – letting the light wander around wherever it likes as long as the longitudinal modes are in the active volume
– we simply restrict current flow to the regions where we want it to go. |
 |
Two laser structures based on these two principles are shown below: |
|
 |
First a "gain-driven" laser. The current
is fed into only a small area by simple geometrical means as shown. Without particular attention to light confinement, we
still get some positive effect, because the index of refraction in the active region is higher than in the surroundings
due to the high electron density there. |
|
|
|
|
|
 |
Next, an "index driven" laser.
As you can see, it is actually also gain driven to some extent. |
|
|
|
| |
© H. Föll (Semiconductors - Script)