6.2.2 Modes

6.2.2 Laser Modes

This module is not finished but you can get a rough idea of what it's all about.

The Fabry Perot resonator introduced in chapter 6.1.3 is an oversimplification of the situation in a real semiconductor Laser.

Without mentioning it, we have assumed an infinitely extended system in the illustrations, i.e. a one-dimensional situation.

The active region in a real Laser, however, is finite. Often, it consists of a particular material embedded in an other material with a different index of refraction; in any case it ends somewhere. In a most simple approximation we may consider it to be a box of length l, thickness d and width w.

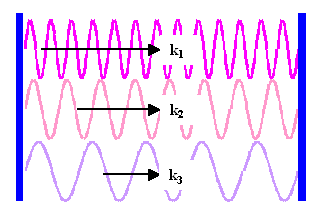
This simply means that many standing waves - with different wavelengths and different wave vector directions - satisfy the resonance condition.

In other words - and that is the common lingo - the Laser cavity may contain many internal modes and thus does not automatically emit monochromatic light in one direction only.

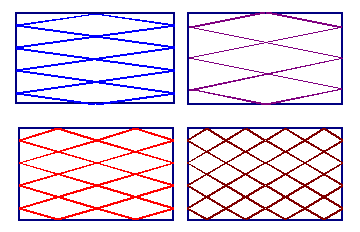
We may distinguish between axial or longitudinal modes, and transverse modes. The figures below illustrates this

Longitudinal Modes

Transverse Modes

Many wavelengths fit in the longitudinal direction which we define to be the direction where we want emission We have
l = m ·l/2n_r and m = 1,2,3,...

Many transverse modes are possible as shown. They are undesirable and should be avoided.

Only wavelengths compatible with the band gap energy, i.e. l = c/n_r·n » c · h/n_r · E_g » µm will become amplified, i.e. m is large since l is typically many µm.

The distance between allowed frequencies is Dn = c/2l · n » 80 GHz for l = 500 µm. The emission lines of the longitudinal, modes are thus very close together.

Laser modes, what to do with them, and how to make a Laser working in only one mode - this is what we naively expect a Laser to be - is clearly a science in itself.

We will not go into details, suffice it to say that monomode Lasers are possible by optimizing the resonating properties of the cavity to the local gain inside it.