Junction Diodes With Small Dimensions

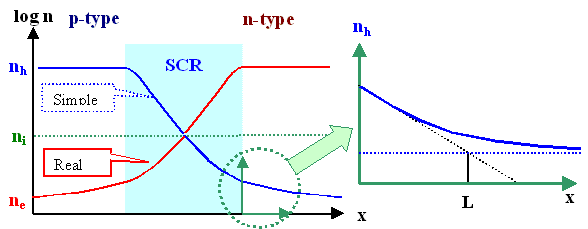
	Lets first look at the basic situation as we had it before for large diodes:
	We have an excess of minority carriers at the edge of the space charge region stemming form the majority carriers injected into the other part of the junction.
		The difference of the actual concentration np,ne,h(U) and the equilibrium concentration np,ne,h(U = 0) was given by
		D np, ne, h ÷ ÷ edge SCR  =  n p, ne, h(U) – n p, ne, h(U = 0)  =   np,ne,h(equ) · æ ç è exp  U kT   –  1 ö ÷ ø
	Neglecting the – 1 for forward conditions, we have the exceedingly simple general relation that the current flowing is simply the diffusion current at the edge of the SCR following from the concentration gradient via Ficks 1st law. Lets look at this a bit closer.
		All that counts is the slope dDnmin/d x of excess minority carrier concentration at the edge of the SCR. It gives directly the minority carrier current at the edge of the SCR - and that is the only current we need to consider.
		Since it is the only component of the current flowing at this point of the junction, (we neglected the other principal terms for the forward condition), and since the current is constant throughout the junction, it simply is the current. We don't have to worry about the other side of the junction or anything else.
		The junction current j thus is
		j  =  – q · D · dDnmin dx ÷ ÷ edge SCR
	What about the current deeper in the Si? The slope is smaller and this must lead to a smaller current, too. Yes - but now we have a majority carrier current, too. Whatever we loose due to recombination in the minority carrier current component, we gain in the majority carrier current component and the total current stays constant.
	In order to compute it, we need the slope and thus Dnmin(x).
		We always obtain D nmin(x) as the solution of a diffusion problem, taking into account boundary conditions, e.g. D nmin(x = 0), i.e. at the edge of the SCR, or the disappearance via recombination.
		One boundary condition is clear: At the edge of the SCR the excess concentration will be at a fixed value controlled by the applied potential as described above .
		The second boundary condition is less clear. When we derived the relation
		Dn(x)  = D n0 · exp – x L
		we also got the current
		j min(x = 0)  =  q · D L · Dnmin(x = 0)
		we implicitly assumed that the size of the diode was infinite and that minority carriers simply disappear by recombination.
	For a small diode now, with x-dimensions much smaller than L, we have to reconsider the diffusion problem.
		Assuming that after a distance dCon << L we now have an ohmic contact, we must ask what the excess minority carrier density will be at x = dCon .
		To make life easy, we now simply include in the definition of a "good" ohmic contact that minority carriers reaching it will recombine instantaneously. While this is pretty much true for real contacts, it is not necessarily obvious.
		With this assumption we simply have as the important boundary condition for a small diode .
		Dn(x = dCon)   =   0
	This makes the solution to the diffusion problem very simple.
		Since practically no recombination in the bulk will take place - all minorities die at the contact - the current everywhere is simply the minority carrier current. This necessitates that
		dD nmin dx  = const =  –   Dnmin ÷ edge SCR dCon
		The current then is
		j min  =  j =  –  q · D · dDnmin dx ÷ ÷ edge SCR   =   q · D dCon  · Dnmin (x = 0)
	This is exactly the same formula as for the large diode - except that we now have dCon instead of L as the important length scale of the device.
		Moreover, minority carriers will now disappear by recombination at the contact after an average time ttrans called transit time given by the time they need for traveling the distance dCon. Obviously, we have
		dCon   =  æ è D · ttrans ö ø 1/2
		in complete analogy to the relation between lifetime and diffusion length
	Of course, this is still a rather simple description of a small diode. We only restricted one dimension, since we still treated a one-dimensional case.
		Real diodes might be small in more than one dimension, and all kinds of other complications can be imagined. Nevertheless, the device dimensions and the transit time will in one form or other replace the bulk diffusion length and lifetime.
		The importance of this can not be overestimated. Device sizes in integrated circuits are in the sub-µm region and critically influence device behavior.

With frame

3.4.1 Junction Diodes

3.3.2 Scaling Laws

© H. Föll (Semiconductors - Script)