Band Diagram Construction for the Free Electron Gas

In order to just understand how the multi-branched band structures always found in all semiconductor books are constructed, it is sufficient to combine the free electron gas model with the reduced band diagrams.

In other words, we assume a periodic potential with infinitely small amplitude - we have the full implications of Blochs theorem, but the dispersion curves from the free electron gas are unchanged.

The old energy - wave vector relation E( k) = (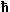²/2m) · k² may be replaced by its periodic version in reciprocal space

E(k + G)	=	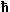² 2m	·	(k + G)²

Since the reduced band diagram simply prints the E(k + G) values in the interval k = 0 to k = 2p /L_G with L_G signifying the extension of the 1st Brillouin zone in the direction of G , we may write

E_G(k + G)	=	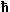² 2m	·	(k + G)²

with the subscript G showing that we consider the dispersion curve along a certain direction in reciprocal space.

Reciprocal space can be tricky; if you understand German here is a link with some details.

The trick is that we can pick any reciprocal lattice vector and add it to the k -vectors that are pointing in the chosen direction, and thus generate a whole system of dispersion curves.

Now a simple example:

Lets take the [100] direction in reciprocal space for a bcc crystal. i.e. the G — H direction as the direction for the k - vectors. This is simply one of the the k_x,y,z directions in the old free electron gas model, lets say the k_x direction. The values of k_x range from 0 to 2p/ a with a = lattice constant in real space.

The dispersion relation can now be written as

E(k )	=	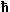² 2m	·	æ ç è	2 p a	· x · i_x	+ G	ö ÷ ø	2

With x = scalar space variable in reciprocal space, restricted to the interval (0, 1), and i_x = unit vector in x-direction in reciprocal space.

All we have to do now is to insert all possible values of G and see what we get.

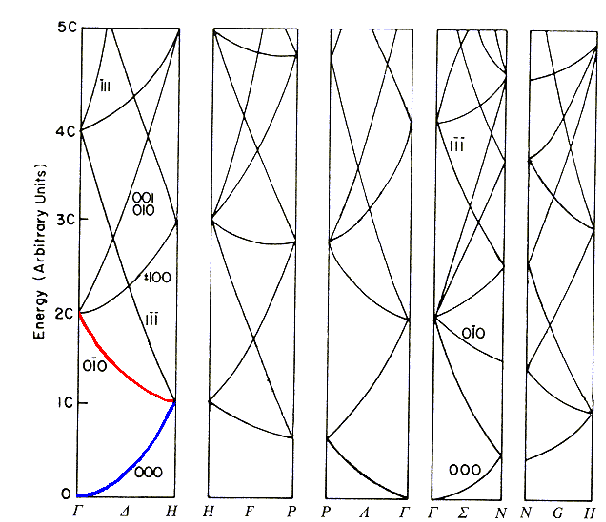
For G = [000] we have the old dispersion relation:

E_[000] (k)	=	² 2m	·	æ ç è	2p a	ö ÷ ø	2	·	æ è	x · i_x	ö ø	2	:=	C · x²

For the sake of clarity we indexed E with the representation of the reciprocal lattice vector describing this branch of the dispersion function. What we get is of course the blue branch in the band structur diagram shown below

Now we take a non-vanishing reciprocal lattice vector, e.g. G = [0,-1,0]. We first express G in terms of the lattice obtaining

G	= –	2 p a	· (i_x + i_z)

Now we evaluate the dispersion relation. We obtain

	E_[0–10]	=	² 2m	·	æ ç è	2 p · x · i_x a	–	2p · (i_x + i_z) a	ö ÷ ø	2

	E_[0–10]	=	C · {i_x · (x – 1) - i_z }²	=	C · (x² – 2x + 2)

In the allowed interval for x we thus obtain a parabolic branch with defined end points at x = 0 and x = 1

E_[0-10] (x = 0) = 2C

E_[0-10](x = 1) = C

This is the red branch in the diagram below

If we continue the procedure, we obtain the complete reduced band diagram for the G — H branch and for all other branches we care to compute. This is shown below.

Adding ± [100] simply means that we move in k - direction into the second Brillouin zone. Indeed, we get the continuation of the G — [000]-H branch - but folded back into the first Brillouin zone as it should be.

With frame

2.1.5 Band Structures and Standard Representations