Depletion

	This is the case where an electrical field of arbitrary origin repulses the majority carriers and a space charge region develops.
		Starting with the Poisson equation for doped semiconductors and all dopants ionized, we have
		d2(DEC) dx2  =  –   e2 · N ee 0 æ ç è 1  –  exp –  DEC kT ö ÷ ø
		In contrast to the case of quasi-neutrality , we now have +DEC >> kT and the sign is important!
	This leads to a simple approximation:
		exp – D EC kT   »  0
		The Poisson equation for the part of the semiconductor that contains this carrier density reduces to
		d2(DEC) dx2  =  –   e2 · ND ee 0
	We have treated this case already in the more basic considerations. The result was
		U(x)  =  e · ND 2ee 0  · x2 –  2dSCR · x + dSCR2 dSCR  =   1  e  ·  æ ç è 2DEC(x = 0) · ee0 ND ö ÷ ø 1/2
		With D EC(x = 0) = DE for brevity, we can rewrite the expression for the width of the space charge layer in terms of the Debye length LDb
		LDb  =  æ ç è e e0 · kT) e2 · ND ö ÷ ø 1/2
		and obtain
		dSCR  =  LDb ·  æ ç è 2DE kT ö ÷ ø 1/2
		If we express DE in terms of the the voltage U between the ends of the sample by e · U = DE, we have the final result
		dSCR  =  LDb ·  æ ç è 2 · e · U kT ö ÷ ø 1/2
	Remember that LDb is a purely material related quality and thus a constant for a given semiconductor. The width of the space charge region can be expressed very simply in terms of LDb , it is always larger by the factor {2eU/kT}1/2
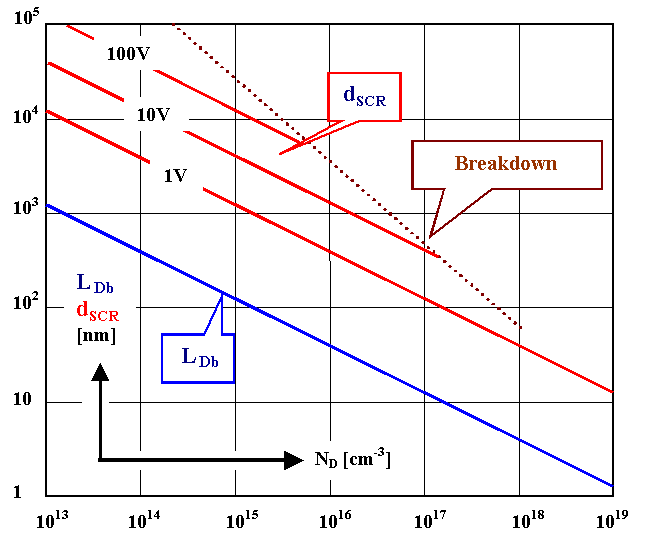
		Since kT at room temperature » 1/40 eV, while applied voltages may be up to 1000 V, dSCR may exceed LDn by several orders of magnitude. This is shown in the illustration below (the numbers are basically correct, but not in detail).
		The breakdown limit indicates that the SCR, being an dielectric insulator, will eventually experience electrical breakdown if the field strength exceeds an upper limit.

With frame

2.3.4 Useful Relations

Space Charge Region and Poisson Equation

Band-Bending and Surface Charge

Debye Length

© H. Föll (Semiconductors - Script)