|
Es gibt keine elementaren magnetische Monopole – wohl aber elementare magnetische Dipole: |
|
|
|
| mAtom |
= |
S mBohr |
= |
kleinst-
möglich |
|
Geradzahliges z Þ
mAtom = 0
Ungeradzahliges z Þ
mAtom = (1, 2, 3, ...) · mBohr |
|
|
 |
1. Ein magnetisches Bahnmoment
mBahn, das aus dem "Strom" der Elektronen resultiert, die "im Kreis"
um einen Atomkern "fliessen" | |
|
 |
2. Ein magnetisches Spinmoment, d. h. ein mit dem Spin der Elektronen gekoppeltes magnetisches
Moment, das die Elektronen schlicht "haben". | |
|
 |
Beide sind ±1
Bohrsches Magneton groß. |
|
 |
Das magnetische Moment eines Atoms kommt von der Überlagerung der Bahn- und
Spinmomente und tendiert dazu, so klein als möglich zu sein. |
|
|
 |
Damit hat aber die Hälfte der Atome (alle mit ungeradzahligem z) mindestens
ein mBohr. | |
| | |
| |
|
 |
Wichtig: magnetische Momente der Atome können
in jede Richtung zeigen und diese Richtung auch ändern, ohne daß das im Kristall
fest gebundene Atom sich drehen muss! |
|
|
|
 |
Bei elektrischen Dipolmomenten geht das nicht! |
|
|
| |
| |
 |
Im magnetischen Feld gibt es zwei grundlegende
Materialeffekte: | |
| Diamagnetische Materialien |
Minimaler Effekt.
Vollständig uninteressant für ET&IT
Wird nicht weiter
behandelt | | Paramagnetische Materialien |
|
|
 |
In Atomen / Kristallen ohne magnetisches Moment der Atome
werden durch ein magnetisches H-Feld welche induziert (Analogon bei Dielektrika: Elektronenpolarisation). |
|
|
 |
In Atomen / Kristallen mit magnetischem Moment der Atome
werden diese Moment im H-Feld etwas ausgerichtet |
|
 |
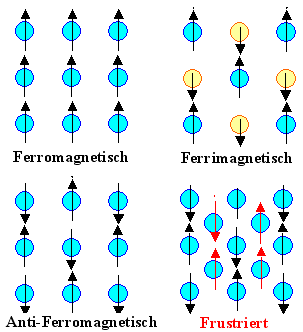
Interessant sind nur ferromagnetische Materialien,
bei denen zwischen den magnetischen Momenten der Atome eine so starke Wechselwirkung besteht, dass eine Ordnung in den sonst
statistisch verteilten Richtungen der magnetischen Momente auftritt. |
|
|
|
 |
In den technisch sehr wichtigen ferromagnetischen Materialien (Fe, Co, Ni)
zeigen die magnetischen Momente alle in dieselbe Richtung, Der Nettoeffekt ist starke Magnetisierung
. | |
|
 |
In den technisch unwichtigen anti-ferromagnetischen Materialien (Cr) zeigen magnetischen
Momente abwechselnd in entgegegesetzte Richtung. Der Nettoeffekt ist keine Magnetisierung |
|
|
 |
In den technisch sehr wichtigen ferrimagnetischen Materialien bleibt trotz antiferromagnetischer
Grundstruktur eine Nettomagnetisierung, da die antiparallelen Momente ungleich groß sind.Þ |
|
 |
Die formale Beschreibung folgt der Systematik bei den Dielektrika. |
|
| B | = |
µo · H + J = µo
· (H + M) |
| M | = |
J/ µo = (µr - 1) · H
= cmag · H |
|
|
|
 |
Primäre Materialparameter sind die magnetische Polarisation
J oder die Magnetisierung
M sowie die magnetische Suszeptibilität
cmag. | |
|
 |
Für Ferromagnetika ist allerdings M nur für kleine Magnetfelder proportional
zu H; die Angabe einer konstanten
magnetischen Suszeptibiltät ist also nur bedingt sinnvoll. |
|
| |
| |
|
 |
Viele ferromagnetische Materialien haben trotz paralleler Ausrichtung der atomaren
magnetischen Momente eine verschwindende Magnetisierung, d. h. sie sind keine starken Permanentmagnete. |
|
|
|
 |
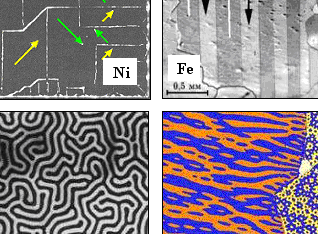
Der Grund dafür liegt in der Ausbildung von magnetischen
Domänen
= Bereichen mit perfekter magnetischer Ordnung, aber mit verschiedener, sich insgesamt weitgehend aufhebender Ausrichtungen
der Magnetisierung. | |
|
 |
Die Domänenwände sind flächige Defekte
im Ordnungsmuster der atomaren Magnetisierungen und haben somit eine Energie pro cm2 |
|
|
 |
Die Magnetisierung über eine Domänenwand ändert sich stetig; damit haben Domänenwände
eine "Dicke", die viele Gitterkonstanten betragen kann. | |
| | |
| |
 |
Es gibt zwei Hauptarten von Domänenwänden: die Blochwand
und die Neélwand . | |
|
|
 |
Meist liegen Blochwände vor; Neélwände sind eher in dünnen Schichten
prominent. | |
|
| | | |
 |
Domänen entstehen, weil durch Domänenbildung trotz des Energieinvestments
für die Domänenwände, die (freie) Energie des Materials ingesamt gesenkt werden kann. Dabei sind drei Energiebeiträge
besonders wichtig: | |
- Energie des externen Magnetfelds.
- Verformungsenergie wg. Magnetostriktion
- Anisotropie über "leichte Richtungen"
|
 |
|
| |
| |
|
 |
Im sich bis ins "Unendliche" erstreckenden Magnetfeld eines starken Magneten steckt
eine Menge Feldenergie. Mit geeignet angeordneten Domänen kann diese Energie praktisch
auf Null reduziert werden. | |
|
 |
Kristalle mit geordneten magnetischen Momenten zeigen ausnahmslos den Effekt der Magnetostriktion
– d. h. sie "ziehen" sich senkrecht zur Magnetisierungsrichtung etwas zusammen. Damit kommt elastische
Energie ins Spiel (Es werden Bindungsfedern gedehnt oder gedrückt). | |
|
 |
Die gemeinsame Richtung der geordneten magnetischen Momente ist nicht beliebig sondern energetisch
am günstigsten für "leichte Richtungen" = niederindizierte kristallographische
Richtung, (z. B. <100> in Fe, <111> in Ni). | |
|
 |
Die resultierenden Strukturen können sehr komplex sein, minimieren aber schlicht die
Energie. | |
|
| | | |
 |
Mit einem äußeren Magnetfeld vergrößern sich günstig
orientierte Domänen auf Kosten der anderen. Þ |
|
|
 |
Dazu müssen sich Domänenwände bewegen.
Domänenwände werden aber in ihrere Beweglichkeit stark von lokalen inneren mechanischen Spannungen / Dehnungen
= Defekten beeinflusst. Das hat eine Reihe von Konsequenzen: |
|
|
 |
Die Magnetisierungskurve wird nichtlinear und zeigt oft Hysterese. |
|
|
 |
Domänenwände zu verschieben geht nicht so schnell. Þ
Die Frequenzabhängigkeit der Magnetisierung von ferromagnetischen Materialien
folgt aus der "Mechanik" der Domänenbewegung, die schon bei relativ niedrigen Frequenzen (kHz . . . MHz)
schlappmacht – außer bei speziellen "Nano"-Werkstoffen. | |
|
 |
Domänenwände hin und her zu schieben kostet Energie. Ein Teil der magnetischen Verluste
P (die Hysterseveluste
PHyst) erklärt sich durch diesen Effekt. | |
|
 |
Kristalldefekte beeinflussen (typischerweise erschweren) die Bewegung von Domänenwänden.
Damit lassen sich Eigenschaften der Hysteresekurve durch "defect engineering" einstellen. |
|
| |
| | |
 |
Weitere Verluste
PWirb resultieren von induzierten Wirbelströmen in leitenden magnetische Materialien (spez.
Widerstand r). | |
| P Fe | = |
PWirb + PHyst |
| | | | | | | |
= |
p · d2
6r |
· (f · Bmax)2 |
+ 2f · HC · Bmax |
|
|
|
 |
Beide Verlustarten sind proportional zur Frequenz f.
d ist die Dicke des Materials senkrecht zur Feldrichtung. | |
|
 |
Zur Minimierung von PWirb ist es angebracht, statt Volumenmaterials
eine Schichtung isolierter Bleche zu nehmen (z. B. Trafokerne) | |
| | |
| |
 |
Anwendungen brauchen entweder hart- oder weichmagnetische Materialien. |
|
|
|
 |
Die paradigmatischen Beipiele für Weichmagnete sind
Transformatorkerne | |
|
 |
Die paradigmatischen Beispiele für Hartmagnete sind
magnetische Speicher. Wir brauchen hier Remanenz
– in der Richtung der Magnetisierung steckt das Bit. |
|
|
 |
Für "richtige" Permanentmagnete (z. B. für Lautsprecher, Mikrowellenröhren,
Generatoren, ...) braucht man selbstverständlich auch ein möglichst hartmagnetisches Material. |
|
| |
| | |
|
 |
Das Maßschneidern von Hysteresekurven (und anderen Eigenschaften) erfolgt
durch: | |
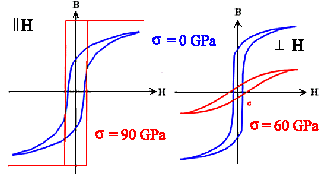 |
Direkter Einfluß mech. Spannungen auf
Hysteresekurven in Ni |
|
|
 |
Optimale Materialwahl
- Ferromagnetische Elemente
und Legierungen:Fe , Ni, Co.
- Kombinationen mit antiferromagnetischen Elementen (Cr, ...)
und "fast" ferromagn. Atomen (Mn, Ga, O, ..
- Moderne "Exoten" mit seltenen Erden: Co Sm, FeNdB,
FeTb, ... | |
|
 |
"Defect Engineering" Beeinflussung der Domänenwandbewegung
durch mech. Spannungen verursacht durch Defekte (Ausscheidungen Korngrenzen, Versetzungen, ...). |
|
|
 |
Faustregel: Defekte machen magn. "härter". |
|
© H. Föll (MaWi für ET&IT - Script)