|
Wir kennen den Ursprung magnetischer Felder und verstehen die Asymmetrie zwischen
magnetischen und (die)elektrischen Eigenschaften. |
|
 |
Die Rolle des Bohrschen Magnetons als elementarer
magnetischer Dipol, auch die Herkunft aus Spin und Bahnmoment der Elektronen einzelner Atome, ist uns geläufig. |
 |
Bei Festkörpern wissen wir: |
|
 |
Entweder haben die den Festkörper konstituierenden Atome keine
magnet. Momente, dann haben wir für die ET&IT uninteressante diamagnetische
Materialien vor uns. |
|
 |
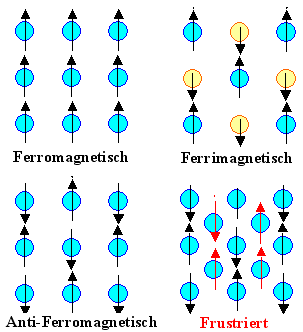
Oder es gibt magnet. Momente. Dann unterscheiden wir:
- Paramagnete = keine Ordnung (bei RT) und für die ET&IT uninteressant,
da auch "Orientierungspolarisation" nur geringe Effekte erzeugt.
- Ferro-, Ferri- und Antiferromagnete
mit magnetischer Ordnung unterhalb einer kritischen Temperatur (Curie-T für "Ferro";
Neél-T für "Antiferro").
|
|
 |
Obwohl Anti-Ferromagnetismus für ET&IT-Anwendungen noch
bedeutungslos ist, wird sich das in der Zukunft ändern ("Spintronic"), deshalb kennen wir den Begriff. |
| |
|
 |
Die formale Beschreibung magnetischer Phämomene ist uns halbwegs geläufig,
auch die Analogie zur Beschreibung von Dielektrika. Die Tabelle im Link
verstehen wir im Prinzip. Insbesondere sind die folgenden Gleichungen klar: |
| |
| B | = |
µo · H + J = µo
· (H + M) |
| M | = |
J / µo = (µr – 1) · H
= cmag · H |
|
|
|
 |
Wir kennen auch die Benennungen: Primäre Parameter sind die magnetische
Feldstärke H, magnetische Induktion
B, magnetische Polarisation
J oder die Magnetisierung
M sowie die magnetische Suszeptibilität
cmag oder die (relative) Permeabilität
mr. |
 |
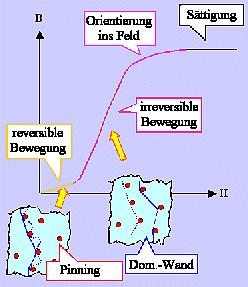
Wir wissen, warum der simple Zusammenhang M = c
mag
· H für Ferromagnete nur sehr bedingt gilt (kleine H bei Ausgangsmagnetisierung
M = 0) und daß wir ansonsten sehr komplexes Verhalten mit Hysteresekurven
bekommen. |
|
 |
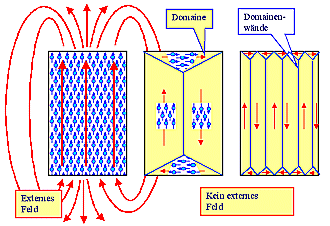
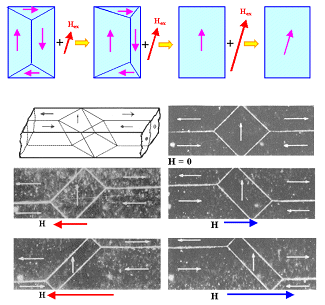
Wir verstehen auch warum. Die Stichworte sind: Domänen, Domänenwände,
Verschiebung von Domänenwänden! Wir können die nachfolgenden Bilder sowohl interpretieren als
auch – der Spur nach – selbst zeichnen |
|
|
|
 |
Die energetischen Gründe für die Entstehung von Domänen sind klar,
auch die Balance zwischen Domänenwandenergie und reduzierter Feldenergie und elastischer Energie; der Begriff "Magnetostriktion " sagt uns was. |
|
 |
Die Bezeichnung "leichte Richtungen " sagt uns
in diesem Zusammenhang auch was. |
 |
Wir verstehen, dass magnetische Verluste aus
zwei Komponenten bestehen – Wirbelstromverluste und Hystereseversluste
–, die beide mit der Frequenz ansteigen (quadratisch für Wirbelstrom, linear für Hysterese). |
|
 |
Wirbelstromverluste lassen sich bekämpfen (wir kennen zwei Methoden: isolierte Bleche
und ferromagn. Isolatoren), Hystereseverluste nicht, sofern man einen hartmagnetischen
Werkstoff braucht, denn sie sind, wie wir wissen, gegeben durch die Fläche der Hysteresekurve. |
 |
Es ist klar, dass nur das Frequenzverhalten
der Ferro-(und Ferri-)Materialien wichtig ist, und dass wir dabei die Zeitabhängigkeit der
Verschiebung von Domänenwänden betrachten. |
|
 |
Damit ist auch klar, dass bei hohen Frequenzen nicht mehr viel passiert. Insbesondere können
wir in der eigentlich korrekten Gleichung für den optischen Brechungsindex n = (er
·mr)½ derzeit noch
mr = 1 setzen. |
 |
Wir können zumindest die paradigmatischen Anwendungen für Magnetwerkstoffe
angeben, nach hart- und weichmagnetisch sortieren und ein paar Möglichkeiten zur Optimierung einer Hysteresekurve angeben
und begründen. |
| |
|
© H. Föll (MaWi für ET&IT - Script)