|
Defekte sind wichtig! |
|
- Viele Eigenschaften sind sensitiv auf Defekte.
- Defekte erlauben Prozessieren.
|
|
| | |
| |
 |
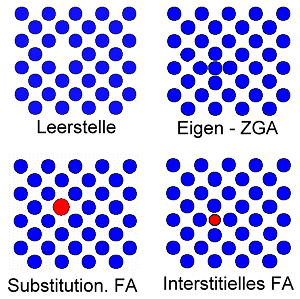
Nulldimensionale Defekte
(oder "Punktdefekte", "Punktfehler",
atomare Defekte)
| |

| | Beispiel: Leerstelle |
|
|
 |
Defekt hat kleinstmögliche Ausdehnung = "null",
d.h. atomare Dimensionen. - Fehlendes Atom = Leerstelle
- Extra-Atome, eigene oder fremde
| |
| |
| | |
|
 |
Eindimensionale Defekte
(oder "Versetzungen",
"Liniendefekte") | |
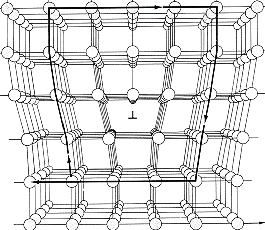
| | Beispiel: Versetzung |
|
|
 |
Entlang einer Linie (die nicht gerade verlaufen muß,
sondern willkürlich gekrümmt oder in sich geschlossen sein kann) ist die Symmetrie
verletzt. | |
| |
| | |
|
 |
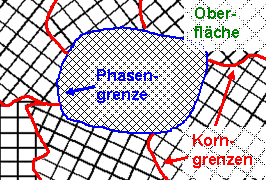
Zweidimensionale Defekte
(oder "Flächendefekte") |
|

| | Beispiel: Korngrenzen |
|
|
 |
Auf einer Fläche (beliebig gekrümmt) ist an
jedem Punkt die Symmetrie verletzt – die Teile rechts und links passen nicht zusammen. - Korngremzem
- Phasengrenzen
- Stapelfehler
| |
| | |
| | |
 |
Dreidimensionale Defekte
(oder "Volumendefekte") |
|
| | Beispiel: Ausscheidung im Polykristall |
|
|
 |
In einem beliebigen Volumen liegt an jedem Punkt eine
andere Symmetrie vor. - Ausscheidungen
- "Hohlräume" (= Voids)
|
|
| |
| | |
|
 |
Es gibt vier Grundtypen atomarer Fehlstellen: |
|
|
|
 |
Die intrinsischen Fehlstellen Leerstelle
(V) und Eigen-Zwischengitteratom (ZGA oder i) sind im thermodynamischen Gleichgewicht
immer vorhanden mit der Dichte n
V,i oder der Konzentration (relative Häufigkeit) cV,i: |
|
|
| |
|
|
|
| nV,i | = |
N0 · exp (– |
EV,i F
kBT |
) |
| | |
| |
| cV,i = | nV,i
N0 | = |
exp ( – |
EV,iF
kBT |
) |
|
| |
|
| |
| |
 |
Die Konzentration steigt also exponentiell mit der Temperatur. |
|
Leerstellen: EV,iF
» (0,5 - 2) eV
ZGA: EV,i
F » (2 - 5) eV
|
|
|
 |
Typische Bildungsenergien EV,iF sind im Bereich von 1
eV . | |
|
 |
Merken:
(kBT) RT = 1/40 eV. | |
 |
Die Konzentration der extrinsischen
AFs ist i.d.R. durch das Ausgangsmaterial bedingt. Sie liegen dann in Über
- oder Untersättigung vor |
|
|
| |
|
 |
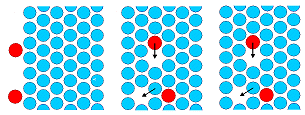
Atomare Fehlstellen sind beweglich. Sie können im Kristall
diffundieren. | |
|
|
 |
Intrinsische und extrinsische ZGA diffundieren direkt durch Sprünge auf äquivalente Nachbarpositionen. |
|
|
 |
Leerstellen diffundieren durch Sprünge der Nachbaratome in die Leerstelle. |
|
|
 |
Substitutionelle Fremdatome diffundieren über einen Leerstellenmechanismus
Þ | |
 |
Diffusion ist eine Grundtechnologie, insbesondere für Halbleitertechnik. |
|
|
| |
|
 |
Entscheidend ist die Sprungrate r. |
|
| r = |
n0 | ·
| exp ( – |
EM
kBT
| ) |
| | Zahl der
Anläufe / s | |
Wahrscheinlichkeit,
dass es klappt |
|
|
|
 |
n0 = Schwingungsfrequenz der Atome im Kristall »
1013 Hz | |
 |
Wesentliche Erkenntnis: Boltzmannfaktor exp[–
E/(kBT)] = Wahrscheinlichkeit
, dass ein Teilchen (eines Ensembles mit der Temperatur T) die Energie E "hat". |
|
|
| |
| |
 |
Makroskopische Diffusionströme
j (= Teichen pro s und cm2) werden durch Konzentrationsgradienten Ñc getrieben. | |
| jx | µ
| ¶ n(x,y,z)
¶x | | | | |
| j( r) | = |
– D · Ñn(r) |
| D(T) |
= |
a2 · r(T) | =
|
a2 · n0
|
· exp (– |
EM
kBT |
) | | |
| |
| |
| |
| | = |
D0 · exp (
– | EM
kBT |
) | |
|
|
|
 |
1. Ficksches Gesetz koppelt Ströme und Gradienten. |
|
|
 |
Diffusionskoeffizient
D beschreibt Teilcheneigenschaften (a = Gitterkonstante). Typische Wanderungsenergien
EM (M = "migration") sind im Bereich von 1 eV. |
|
|
 |
2. Ficksches Gesetz beschreibt die zeitliche Änderung der Konzentration.
| |
|
| |
|
|
|
¶n
¶t | = D · |
æ
ç
è |
¶2n
¶x2 | + |
¶2n
¶y2 | + |
¶2n
¶
z2 | ö
÷
ø |
= D · Dn |
|
| |
|
| |
|
|
 |
Diffusionsströme geladener Teilchen sind elektrische Ströme! | |
| | |
| |
|
 |
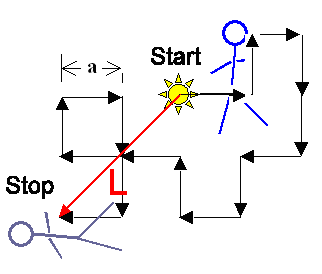
Diffundierende Teilchen machen einen "random walk": |
|
|
|
 |
Zwischen Schrittweite (meist » Gitterkonstante a),
Zahl der Schritte N, Diffusionskoeffizient D, "Laufzeit" t
und der Diffusionlänge
L gibt es einfache Zusammenhänge: | |
| |
| |
| |
| |
|
| |
|
|
 |
Die letzte der beiden Gleichungen muss man wissen! |
|
| |
| |
| |
 |
Praktisch alle Kristalle enthalten Versetzungen in einer Dichte |
|
Die plastische Verformung aller Kristalle
(= aller Metalle) erfolgt ausschließlich durch
die Erzeugung und Bewegung von Versetzungen |
|
| |
| r | = |
Gesamtlänge Versetzungen
Volumen Kristall |
|
| |
|
| |
|
|
 |
"Gute" Einkristalle
(Labor): r
» (103 bis 105) cm–2. |
|
|
 |
Normale Kristalle inkl. Polykristalle: r
» (105 bis 109) cm–2 |
|
|
 |
Stark verformte Kristalle:
r bis 1012 cm–2. |
|
|
| |
|
 |
Materialentwicklung Strukturwerkstoffe (Stahl, Alukarosserie, Turbinenschaufeln,
...) Þ | |
Metalltechnik =
Beeinflussung der Erzeugung und Bewegung
von Versetzungen durch andere Defekte |
|
|
 |
Ohne Versetzungen keine Metallurgie! |
|
|
 |
Mit Versetzungen Probleme bei elektronischen Eigenschaften. |
|
| |
| |
| |
 |
Mikroelektronik braucht versetzungsfreies Silizium! |
| |
| |
 |
Herstellung komplett versetzungsfreier
Si-Einkristalle ist eine hohe Kunst! | |
|
| | |
| | |
© H. Föll (MaWi für ET&IT - Script)