Lösungen zur Übung 3.1-1:

Kristalle

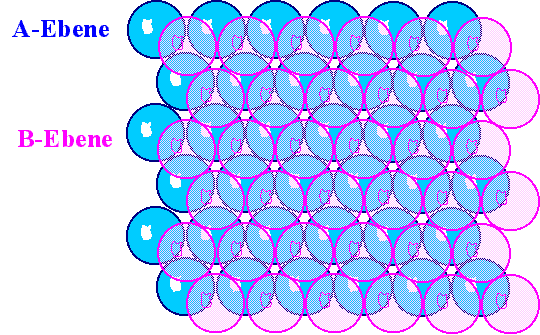
	Frage 1: Für eine dichteste Kugelpackung müssen die Kugeln = Atome auf einer Ebene so wie nebenstehend gezeigt angeordnet sein. Wie es dreidimensional weitergehen muss ist auch klar.Wie paßt das zu einem kubisch flächenzentrierten Gitter?
		Die roten Punkte unten links markieren das fcc Gitter. Setzt man Atome erstmal nur auf die Gitterpunkte, die die eingezeichnete Raumdiagonalebene aufspannen, wird das charakteristische Sechseck der dichtesten Kugelpackung in einer Ebene sichtbar.
		Startet man die Raumdiagonalebene beim nächstgelegenen Atom (das in der Flächenmitte), sitzen die dann erfaßten Atom exakt in den Kuhlen der Nachbarebene; uns so weiter - wir haben damit dichteste Kugelpackung.
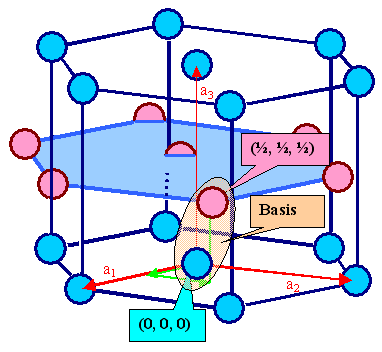
	Frage 2. Die Kombination von 2 identischen Atomen in der Basis (eines bei (0,0,0) das andere bei (½,½ ,½) mit einem hexagonalen Gitters ergibt ebenfalls eine dichteste Kugelpackung. Wie?
		Das Bild unten rechts zeigt das im Detail.
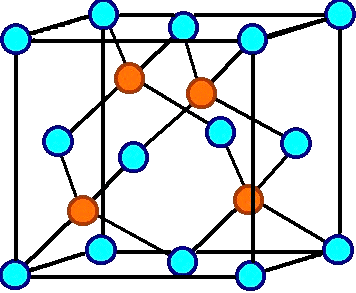
	3. Die Kombination von 2 Atome in der Basis (bei (0,0, 0) und (¼, ¼, ¼) ) mit dem kubisch flächenzentrierten oder fcc (face centered cubic) Gitter ergibt keine dichteste Kugelpackung dafür die Grundstruktur der meisten Halbleiter - Si, Ge, GaAs, InP. Erläutere
		Wenn an die grünen Atome vom Bild oben links auf eine Eben zeichnet, fortsetzt, und dann noch die nächste Atomlage gleich draufsetzt, ergibt sich das Bild unten rechts:
		Die zur Abwechslung jetzt blau gemalten Atome entsprächen den grünen Atomen vom ersten Bild, die pinken der nächsten Lage. Im Bild daneben wären dann nur blaue Atome präsent.
		Im Si Kristall (oder allgemeiner: in Kristallen mit Diamantstruktur) wie oben rechts gezeigt, sind aber für die sonst dichtest gepackten Ebenen noch die roten Atome dazwischen - das kann dann keine dichteste Kugelpackung mehr sein.

Mit Frame

Übung 3.1-1

© H. Föll (MaWi für ET&IT - Script)