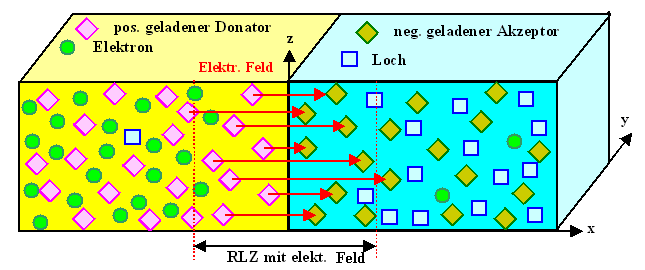
| |
 |
Hier nochmal die Ortsdarstellung des pn-Übergangs; um etwas allgemeiner
zu sein, nehmen wir an daß die p-Dotierung etwas größer ist als die n-Dotierung |
| |
|
|
Jetzt zur qualitativen Lösung der Poisson Gleichung: |
| |
|
 |
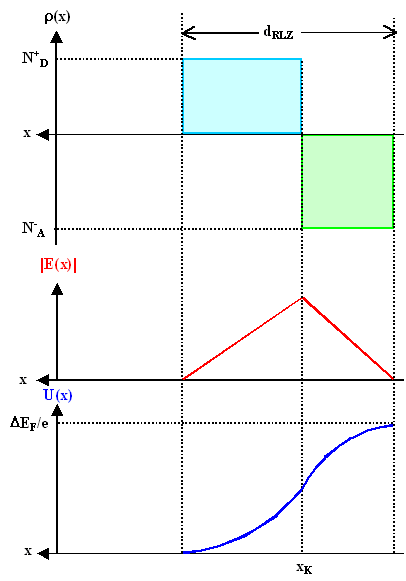
Wir starten wie gehabt
mit der Ladungsgverteilung; sie sieht dann (leicht idealisiert) so aus wie nebenstehend gezeichnet. |
|
|
|
|
Die Flächen der beiden (idealisierten) Rechtecke muß natürlich gleich sein
(das ist eine Randbedingung), da wir ja gleichviel positive und negative Ladungen brauchen. |
|
|
Einmal integrieren ergibt die Feldstärke; sie hat ihr Maximum am Ort des Kontakts, aber
für verschiedene Dotierkonzentrationen ist die Steigung (der Gradient der Feldstärke) verschieden. |
|
|
Weit weg vom Kontakt ist sie Null; am Kontakt gleich groß - wieder haben wir Randbedingungen. |
|
|
Die zweite Integration ergibt das Potential, es ist aus Parabelstücken zusammengesetzt.
Links ist "geerdet, d.h. das Potential (willkürlich) auf Null gesetzt- eine weitere Randbedingung. |
| |
|
|
Die quantitative Lösung der Poissongleichung startet also mit obigen Randbedingungen
und den Ausgangsgleichungen |
| |
|
|
|
|
| |
|
|
|
Wobei F die Fläche des Kontakts ist, und dRLZ(±)
der jeweilig Anteil der RLZ n- bzw. p-Gebiet. |
|
|
Die Rechnung ist nicht schwierig, macht aber doch einige Schreibarbeit. Wer sehen will wie es geht, betätigt den Link. |
| | |
|
© H. Föll (MaWi 2 Skript)
Mit Frame
6.2.1 Der pn-Uebergang