|
Unter Ermüdung verstehen wir Änderungen
der Materialeigenschaften, die durch ständig wechselnde kleine Belastungen (z.B.
Vibrationen und Schwingungen) verursacht werden, und die im Extremfall einen plötzlichen und oft katastrophalen Bruch
verursachen. |
|
 |
Entscheidend (und zunächst unverständlich) ist dabei, daß Ermüdung auch
eintreten kann, falls die Amplituden der Schwingungen, und damit auch die im Material auftretenden Spannungen, weit unterhalb der Fließgrenze bleiben, so daß eigentlich nur elastische
Verformung vorliegen sollte. |
|
 |
Wenn trotzdem plastische Verformung stattfindet, ist klar, daß
wir eine Abhängigkeit des Ermüdungsphänomens von der Frequenz und der Amplitude der Wechselbelastung erwarten
müssen. Damit ist schon im einfachsten Fall einer Dauerbelastung mit konstanter Frequenz und Amplitude komplexes Verhalten
zu erwarten, das selbstverständlich auch noch vom Gefüge des gegebenen Materials abhängen wird. |
|
 |
Schwanken Frequenz und Amplitude auch noch im Laufe der Zeit, wird die Sache vollends unübersichtlich,
da sich die Effekte nicht einfach addieren lassen. |
 |
Wenn ein Material das jahrelang gehalten hat und von dem wir sicher sind, daß es ursprünglich
keine Mikrorisse enthielt, durch Ermüdung ohne Vorwarnung und ohne große plastische Verformung plötzlich
bricht, müssen wir davon ausgehen, daß sich im Laufe der Zeit Mikrorisse gebildet haben, die l a
n g s a m gewachsen sind, bis dann einer die für die vorliegende Belastung definierte kritische Größe
erreicht hat. |
|
 |
Damit müssen wir primär nach Mechanismen suchen, die zur Bildung und langsamen Wachstum von Mikrorissen
bei Wechselbelastung (und nur bei Wechselbelastung)
führen. |
|
 |
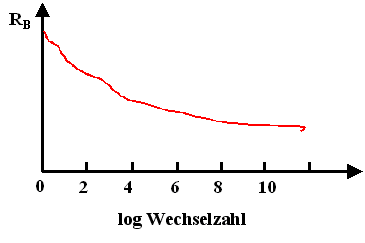
Leider gibt es keine einfache Antwort. Was man beobachtet, wenn man
in Ermüdungsexperimenten eine Probe zyklisch verformt, ist eine mit der Zahl der Zyklen kontinuierlich abnehmende maximale
Zugfestigkeit oder Bruchspannung RM (das war der Wert
des Maximums in der Spannungs-Dehnungskurve). Trägt man für eine gegebene Amplitude der Schwingungsbelastung
RM gegen die Zyklenzahl auf, erhält man die sogenannte Wöhler
- Kurve. Sie sieht typischerweise so aus: |
|
|
|
 |
Der Mechanismus der Ermüdung ist äußerst komplex und längst
nicht im Detail verstanden.. Es lassen sich jedoch zwei fundamentale Mechanismen prinzipiell unterscheiden: |
|
 |
1.
Irreversible Vorgänge bei der Vor- und Rückwärtsbewegung von Versetzungen,
die im Laufe der Lastwechsel zu fundamentalen Änderungen der Versetzungsanordnung führen. |
|  |
2. Durch diese spezielle Versetzungsanordnung entstehen Mikrorisse, meist auf der Oberfläche
des Materials, die solange wachsen, bis die kritische Rißlänge an einer Stelle erreicht ist und das Material
bricht. |
 |
Schauen wir uns diese beiden Mechansismen in einem extrem vereinfachten und idealisierten Modell
kurz an. |
|
 |
Überlegen wir uns zunächst, wie die Versetzungen beim ersten Spannungszyklus am Maximum der Amplitude
vorliegen. Da wir unterhalb der Fließgrenze arbeiten, sind sie an Hindernissen verankert und bewegen sich nicht. |
|
 |
Wechselt die Belastung jetzt von Zug nach Druck, will die Versetzung zurücklaufen, und das kann sie
auch. Denn die Ausscheidungen, an denen sie bei Zugbelastung festhängt, blockieren die Rückwärtsbewegung
nicht. Sie läuft jetzt soweit zurück, bis sie an anderen Auscheidungen wieder
festhängt. |
|
 |
Für den Fall einer einzigen Versetzung sieht das bei Verankerung an Ausscheidungen beipielsweise so
aus: |
| |
|
© H. Föll (MaWi 1 Skript)