 |
Angenommen, in einem (würfelförmigen)
Volumen sind beliebig viele statistisch verteilte gerade Linien (= Versetzungen), die alle parallel zu den Würfelkanten
verlaufen und damit immer an irgendeiner Oberfläche beginnen und enden. |
|
 |
Zeige, daß die Versetzungsdichte dann durch die Dichte
der Durchstoßpunkte der Versetzungen an den Oberflächen gegeben ist; d.h. die Flächendichte
der Durchstoßpunkte ist ist direkt korreliert zur Gesamtlänge pro Volumeneinheit. |
 |
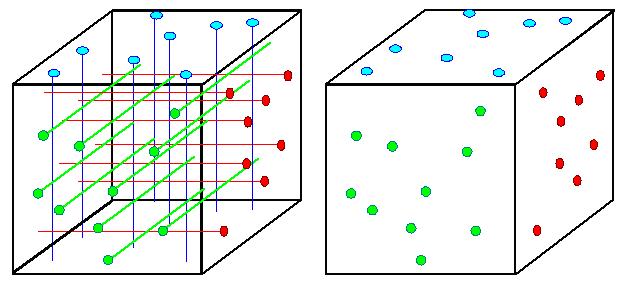
Die erste Frage ist relativ trivial; das Bild macht das klar: |
| |
|
|
 |
Die Gesamtlänge der Versetzungen ist gleich der Zahl der Durchstoßpunkte N
(nur auf einer Fläche gezählt) mal Kantenlänge a des Würfels mal 3 um die anderen
Flächen zu berücksichtigen. Wir haben also für die Versetzungsdichte r |
| |
| r = |
3 · N · a
a3 |
= | 3 · N
a2 |
|
|
|
 |
Die Flächendichte der Durchstoßpunkte ist also bis auf den Faktor 3 identisch
mit der Versetzungsdichte. |
| |
| |
 |
Überlege, ob diese Gleichheit auch noch gilt, wenn die Versetzungen
beliebig gekrümmt laufen dürfen, insbesondere sogar geschlossene Ringe bilden können? |
 |
Die Gleichheit Flächendichte = 1/3 Volumendichte gilt in diesem Fall
nicht mehr in voller Allgemeinheit. |
|
 |
Das ist leicht zu sehen; man muß sich nur einige geschlossene Versetzungsringe im Volumen
vorstellen. Die Flächendichte ist dann = 0, die Volumendichte aber nicht. |
|
 |
Auch für "krumme" Versetzungen, deren Länge zwischen den Durchstoßpunkten
> a ist, kann die Beziehung offenkundig nicht völlig korrekt sein. |
| | |
 |
Ändert sich etwas, wenn wir statt der Dichte der Durchstoßpunkte
auf der Oberfläche des makroskopischen Körpers, die Dichte der Durchstoßpunkte
auf einer beliebigen (gedachten) Ebene durch den Kristall nehmen? |
 |
Ja, das ist eine neue Situation. Wir schneiden jetzt z. B. auch einige der vorhandenen
Versetzungsringe. |
|
 |
Nehmen wir an, die Dichte der Versetzungsringe ist NRing; ihr mittlerer
Radius rRing. Eine beliebige Ebene schneidet dann N2/3 der Versetzungsringe
(das ist analog zur Flächendichte der Atome zu berechnen;
der mittlere Abstand ist N–1/3, und rRing < N–1/3
vorausgesetzt). Ein Versetzungring macht im Prinzip zwei Durchstoßpunkte; die Dichte an Durchstoßpunkten ist
also 2 · N2/3. |
|
 |
Die Versetzungsdichte eines Ensembles von Ringen wäre jedoch r
= NRing · 2 · p · r; die Dichte der Durchstoßpunkte
ist also nicht identisch mit der Versetzungsdichte. |
|
 |
Identität hätten wir nur falls p · r =
N–1/3, d.h. falls der halbe Umfang der Ringe etwa identisch ist zum mittleren Abstand. |
 |
Das ist auch sinnvoll: Sind die Ringdurchmesser größer als der mittlerer
Abstand, bekommen wir mehr Durchstoßpunkte, sind sie sehr viel kleiner verliert die Angabe einer Versetzungsdichte
als Länge pro cm3 ihren Sinn (sehr viele sehr kleine Versetzungsringe als kleine Versetzungsdichte
zu zählen ist einfach nicht sinnvoll. |
|
 |
Falls wir nicht Versetzungsringe, sondern beliebig gekurvte Versetzungen betrachten, ist die
Lage ähnlich. Die Dichte der Durchstoßpunkte ist nicht identisch mit der Versetzungsdichte, kann aber eine gute
Näherungs sein, falls die Versetzungen nicht ganz "pathologisch" durch den Kristall verlaufen. |
| |
|
 |
Läßt sich daraus ein Rezept für die Messung der
Versetzungsdichte in einem Kristall ableiten (Wir unterstellen, daß man die Durchstoßpunkte sichtbar machen
kann? |
|
 |
Ja!. Bestimme die Dichte der Duchstoßpunkte auf mehreren nicht koplanaren Ebenen (z.B.
durch mehrfaches Anschleifen und neu messen). |
|
 |
Falls man jedesmal in etwa die gleiche Dichte an Durchstoßpunkten bekommt, kann man
mit einiger Sicherheit annehmen, dass: - Die Versetzungen homogen verteilt sind
- Die Dichte der Durchstoßpunkte ein gutes Maß für die tatsächliche Versetzungsdichte ist.
|
 |
Wie man die Durchstoßpunkte
sichtbar machen kann, ist im Hyperskript "Defects" beschrieben. |
| | |
© H. Föll (MaWi 1 Skript)
![]() Übung 4.1-3 Grenzflächenenergie pro Atom
Übung 4.1-3 Grenzflächenenergie pro Atom