|
Wie groß ist die Gitterkonstante a des fcc
und bcc Gitters ausgedrückt in Atomradien r? |
 |
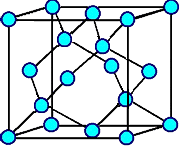
Ein Blick auf die Bravais Gitter
klärt die Geometrie: |
|
 |
Der kleinstmögliche Abstand zwischen zwei Gitterpunkten muß gleich dem doppelten
Atomradius r sein, denn näher können sich zwei Gitterpunkte nicht kommen sobald wir auf jeden Gitterpunkt
ein kugelförmiges Atom mit Radius r setzen. |
|
 |
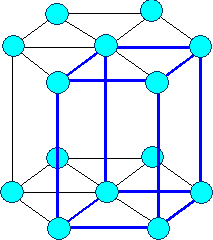
In fcc Gitter findet sich der kleinstmögliche Abstand offenbar entlang der Flächendiagonale,
also entlang einer <110> Richtung. |
|
 |
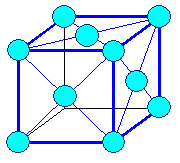
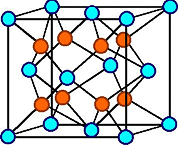
Im bcc Gitter ist es die Raumdiagonale, also die <111> Richtung. |
|
 |
Damit gilt |
|
|
|
 |
Wie groß ist das Achsenverhältnis c/a
für das hexagonale Gitter, falls ein Kristall mit dichtester Kugelpackung erzeugt werden soll? |
 |
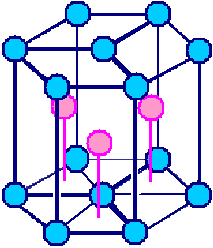
Ein Blick auf das hexagonale Bravaisgitter klärt die Geometrie: |
| |
|
 |
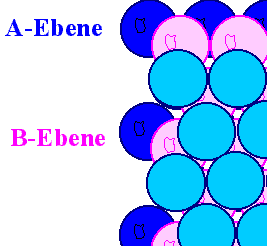
Beide hexagonale Basisebenen sind, in der Nomenklatur der dichtesten Kugelpackung,
A-Lagen. Wir brauchen auf jeden Fall eine Basis mit zwei identischen Atomen, um die für die dichteste Kugelpackung
notwendige B-Lage erzeugen zu können. Damit haben wir die Beziehungen: |
|
 |
Wir haben 2 Atome pro EZ (8 · 1/8 + 1). |
|
 |
Atomradius (= Kugelradius) r = a/2. |
|
 |
Volumen der EZ = a2/2 · 31/2 . c |
|
 |
Packungsdichte
PD = 0.74 |
 |
Damit gilt |
| |
|
| PD = 0.74 | = | 2 · 4/3 · p
r3
a2/2 · 31/2 · c |
= | 16 · p r3
3 · a2 · 31/2 · c |
= | 2 · p a
3 · 31/2 · c |
| c | = | 2 · p a
3 · 31/2 · 0.74 | = 1.633 a |
q.e.d. |
|
 |
Wieviel Atome enthält die Elementarzelle von Ni, Si,
ZrO2? Die Kristalle sind unten gezeigt; die Antwort ist durch Abzählen zu erhalten. |
|
 |
Wieviele Atome hat die jeweilige Basis? |
| |
|
 |
Hier eine tabellarische Übersicht: |
| |
| Ni | Si |
ZrO2 | | Eckatome |
8 · 1/8 = 1 | 8 · 1/8 = 1 |
8 · 1/8 = 1 | | Flächenatome |
6 · 1/2 = 3 | 6 · 1/2 = 3 |
6 · 1/2 = 3 | | Volumenatome | 0 |
4 | 8 | | Summe | 4 |
8 | 12 | | |
Atome in Basis
(Koordinaten) |
1
(0,0,0) |
2
(0,0,0)
(1/4, 1/4,1/4) |
3
(0,0,0)
(1/4, 1/4,1/4)
(1/4, 3/4,1/4) |
|
 |
Die Gitterkonstanten von Ni, Pb und Si sind
3,52 Å, 4.95Å und 5.43Å.Wie groß ist die Dichte? |
 |
Auch hier ist eine Tabelle angebracht |
| |
| Ni | Pb | Si |
Atomgewicht (GA)
( ×
1,66 · 10–27 kg) | 58,7 | 207.2 |
28.1 | | Atome in EZ (AEZ) |
4 | 4 | 8 |
| Gitterkonstante | 3,52 Å | 4.95Å |
5.43Å | | Volumen EZ (VEZ) |
(3,52 Å)3
43,6 Å3
4,36 · 10–23 cm3 |
(4.95Å)3
121.3 Å3
1,21 · 10–22 cm3 |
(5.43Å)3
160.1 Å3
1,60 · 10–22 cm3
| |
| | r [g · cm–3]
| 8.93 | 11.37 |
2.33 |
| Wert aus Tabelle |
8.91 | 11.34 |
2.33 |
|
 |
Das ist nicht schlecht! Die kleinen Diskrepanzen könnte von der unspefizierten
Temperatur herrühren (a ist eine Funktion der Temperatur!) oder von den in realen Metallen (nicht im
Silizium) immer vorhandenen Defekten, die immer die lokale Dichte etwas erniedrigen. |
| | |
 |
Vergleiche die Dichte von Si
in einem Si Kristall mit der Dichte des Si (und nur des Si!) in einem SiO (= Quarz) Kristall.
|
|
 |
Was folgt daraus für die Oxidation von Si? Bedenke,
dass Sauerstoff durch die bereits gebildete SiO2 Schicht diffundieren muß und dann durch "Eindringen"
in das Si Gitter SiO2 bildet. |
 |
Der erste Teil ist kompliziert, aber nicht schwierig, und wird hier nicht ausgeführt. |
|
 |
Das richtige Ergebnis wäre, dass die partielle Dichte nur des Si in SiO2
etwa die Hälfte der Dichte von reinem Si beträgt. |
 |
Was folgt daraus für die Oxidation von Silizium? Das ist die schwierige Frage;
die Antwort hat erhebliche Bedeutung für die Mikroelektronik! |
|
 |
Si oxidiert, falls es Sauerstoff ausgesetzt ist und man eine hinreichend hohe Temperatur
hat. Sauerstoff reagiert mit dem Si zu SiO2 und bildet eine homogene Oxidschicht. |
|
 |
Die einzige Möglichkeit die Schichtdicke zu erhöhen ist offenbar, dass Sauerstoff
durch die bereits gebildete Oxidschicht "diffundiert" und dann an der Grenzfläche Si - SiO2
zu mehr Oxid reagiert. |
|
 |
Ein Volumenelement Si das derart oxidiert produziert dann unvermeidlich etrwa zwei Volumenelemente Oxid, denn die Zahl der Si Atome ändert sich ja nicht, aber
die Dichte ist nur halb so groß. |
 |
Si Oxidation produziert also immer eine erhebliche Volumenvergrößerung
- und das macht jede Menge Probleme in der Mikroelektronik! |
|
| |
© H. Föll (MaWi 1 Skript)