Simple N-dimensional integrals

4.9 Simple N-dimensional integrals

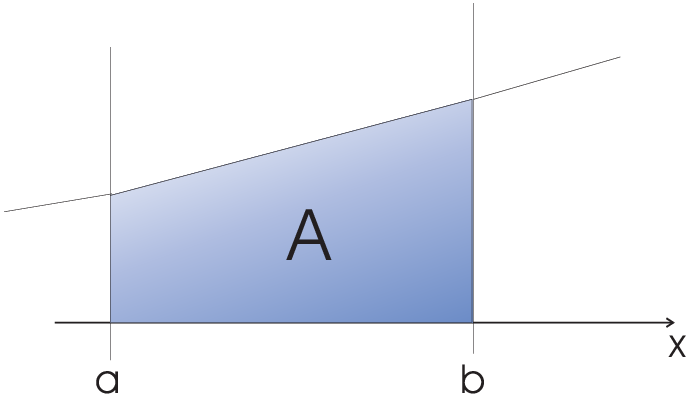\(\left.\begin{array}{c}\int\limits_a^b f(x) dx=A=F(b)-F(a)\\\mbox{with }\frac{dF}{dx}=f(x)\end{array}\right\}\mbox{1D case}\qquad\)

We will only discuss a 3D example: \(f:\mathbb{R}^3\to\mathbb{R}\;\;f(x,y,z)\)
Integrals over volumes:

\[\int\!\!\!\int\limits_V\!\!\!\int f(x,y,z)dx\;dy\;dz=\int\limits_{x_1}^{x_2}\left(\int\limits_{y_1(x)}^{y_2(x)}\left(\int\limits_{z_1(x,y)}^{z_2(x,y)} f(x,y,z)dz\right)dy\right)dx\]

It is often difficult to determine the border, the integrals may be simple. Simplest case: Cartesian limits
Example: \(\quad f(x,y,z)=yxz\) integral over a cube with edge \(a\) \begin{eqnarray*}\int\!\!\!\int\limits_V\!\!\!\int f(x,y,z)dx\;dy\;dz&=&\int\limits_0^a\left(\int\limits_0^a\left(\int\limits_0^a xyz\;dz\right)dy\right)dx\\ &=&\int\limits_0^a\int\limits_0^a\left(\left[xy\frac{1}{2}z^2\right]_0^ady\right)=\int\limits_0^a\left[x\frac{1}{4}y^2a^2\right]_0^a dx =\left[\frac{1}{8}x^2a^4\right]_0^a=\frac{1}{2^3}a^6 \end{eqnarray*}

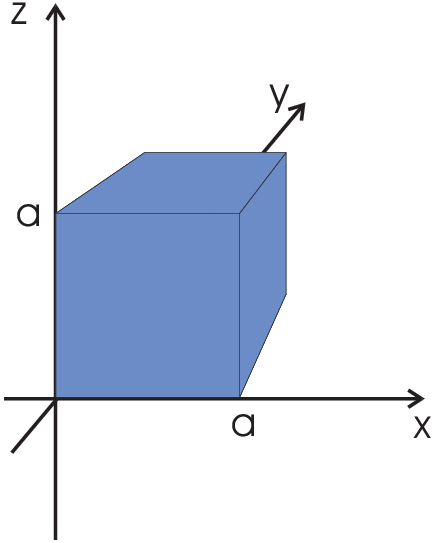
Volume: \(f(x,y,z)=1\to \int\!\!\!\int\limits_\bigcirc\!\!\!\int 1dx\;dy\;dz\hat=\) Volume of the integration area

Example: Volume of a sphere with radius \(R\), i.e. \(R^2=x^2+y^2+z^2\)

\[\begin{array}{l}\iiint\limits_\bigcirc 1\; dx\; dy\; dz\; =\; ? \\ x \in \left[-R,R\right]\\ y \in \left[-\sqrt{R^2-x^2},+\sqrt{R^2-x^2}\right]\\ z \in \left[-\sqrt{R^2-x^2-y^2},+\sqrt{R^2-x^2-y^2}\right]\end{array}\]

Just writing down the limits for the integral is tedious work in Cartesian coordinates, but very simple in spherical coordinates:

\[V = \iiint\limits_\bigcirc 1\;dx\;dy\;dz=\int\limits_0^\pi\int\limits_0^{2\pi}\int\limits_0^R r^2 \sin(\vartheta)\; dr\;d\varphi\;d\vartheta \]

Here we used the Jacobi determinant as calculated in section 4.5.1 to get the correct integration scaling for this coordinate transformation. Finally we get

\[V = 2\pi \left(\left.-\cos(\vartheta)\right|_0^\pi \right) \left( \left.\frac{r^3}{3}\right|_0^R \right) = \frac{4}{3}\pi R^3\]