4.10
Continuity equation using divergency
In this section we discuss local changes of a concentration \(c\) induced
by lateral current flow (and/or local sources or drains). This is illustrated in the following figure for the change of
concentration \(c\) in a (tiny) volume \(A l\) induced by a difference of current flowing into
and out of this volume in \(x\) direction, i.e. in a 1D model. The number of particles entering the
volume at position \(x\) per time \(dt\) is
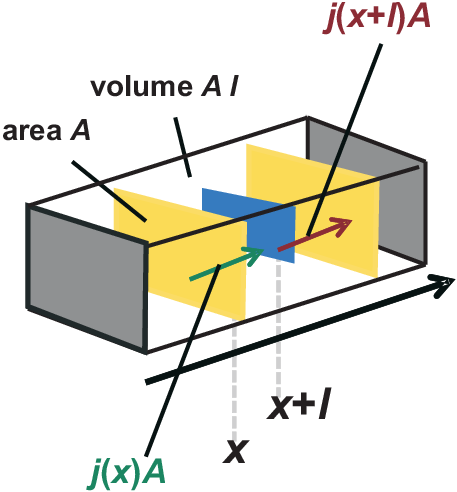
|
| \[ dn^{in} = j(x) A dt \quad . \] |
Correspondingly the number of particles leaving the volume at position \(x+l\) per time \(dt\)
is
| \[ dn^{out} = j(x+l) A dt \quad . \] |
Thus the change of concentration in the volume \(A l\) per time \(dt\) is
|
\[ \frac{dc}{dt} = \frac{dn^{in}-dn^{out}}{A l dt} = \frac{j(x)-j(x+l)}{l} = \frac{j(x)-\left[j(x)+l \frac{dj}{dx}\right]}{l}
= - \frac{dj}{dx}\quad . \label{cont_eq_1D} \] |
|
In 3D and adding local sources and drains we find
|
\[ \frac{dc}{dt} = - \frac{dj_x}{dx}- \frac{dj_y}{dy}- \frac{dj_z}{dz} + sources(\vec{r}) - drains(\vec{r})
= - \vec{\nabla} \vec{j} + sources(\vec{r}) - drains(\vec{r}) \quad . \label{cont_eq_3D} \] |
© J. Carstensen (Math for MS)

