4.5 Total Derivatives

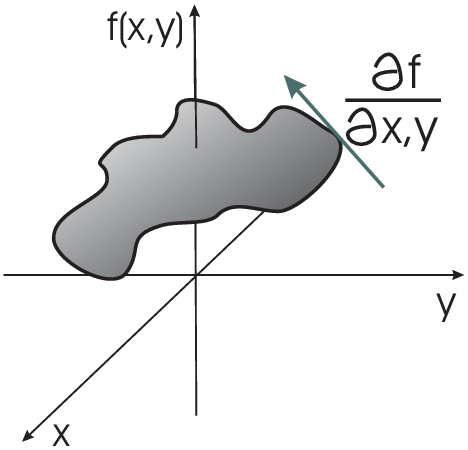
partial derivatives were defined for \(f:\mathbb{R}^n\rightarrow\mathbb{R}^1\)
\(\rightarrow\) tangents on a hyper surface: We consider now:\(f:\mathbb{R}^N\rightarrow\mathbb{R}^M\) a vector function.

Definition 40 \(\vec{f}:\mathbb{R}^N\rightarrow\mathbb{R}^M\;\vec{x},\vec{h}\in\mathbb{R}^N\;\;\tilde{A}\in\mathbb{R}^{M\times N}\;\hat=\;M\times N\) matrix. Matrix \(\tilde{A}(\vec{x})\) is called the total derivative of \(\vec{f}\), if \(\vec{f}\) can be expressed as \begin{eqnarray*} \vec{f}(\vec{x}+\vec{h})&=&\vec{f}(\vec{x})+\tilde{A}\vec{h}+\vec\varphi(\vec{h})\qquad\quad\vec\varphi=\vect{\varphi_1\\\vdots\\\varphi_M}\\ \mbox{where:}\,\lim_{\vec{h}\to\vec0}\frac{\vec\varphi(\vec{h})}{|\vec h|}&=&\vec0\qquad\qquad\qquad\quad\qquad\quad\vec{f}=\vect{f_1\\\vdots\\f_M} \end{eqnarray*}

• total derivative is a Matrix!!

• if \(M=N=1\) then \begin{eqnarray*}f(x+h)&=& f(x)+Ah+\varphi(h)\\ \leftrightarrow\,\frac{f(x+h)-f(x)}{h}&=& A+\frac{\varphi(h)}{h}\\ h \to 0 \Rightarrow \, A&=&\lim_{h\to0}\frac{f(x+h)-f(x)}{h}=f'(x)\Rightarrow\,\mbox{than 1D case o.k.!}\end{eqnarray*}

• in components this means:

  \[f_j(\vec{x}+\vec{h})=f_j(\vec{x})+\underbrace{\sum_{k=1}^N a_{jk}h_k}_{\mbox{Matrix multiplication}}+\varphi_j(\vec{h})\]

• case: \(M=1\): \begin{eqnarray*}f(\vec{x}+\vec{h})&=&f(\vec{x})+\vec{A}\cdot\vec{h}+\varphi(\vec{h})\\ \leftrightarrow f(\vec{x}+\vec{h})-f(\vec{x})&=&\vec{A}\cdot\vec{h}+\varphi(\vec{h})\\ \vec{h}&=&\vect{0\\\vdots\\h\\\vdots\\0}=\vec{e}_kh\\ \rightarrow\,f(\vec{x}+h\vec{e}_k)-f(\vec{x})&=&A_kh+\varphi(\vec{h})\quad\left|:h\right.\\ \frac{f(\vec{x}+h\vec{e}_k)-f(\vec{x})}{h}&=&A_k+\frac{\varphi(\vec{h})}{h}\\ \lim_{h\to0}\frac{f(\vec{x}+h\vec{e}_k)-f(\vec{x})}{h}&=&A_k=\frac{\partial f}{\partial x_k} \end{eqnarray*}

  Thus:

  \[\vec{A}=\vec\nabla f:\;f(\vec{x}+\vec{h})=f(\vec{x})+\vec\nabla f\cdot\vec{h}+\varphi(\vec{h})\]

  is the total derivative \(\rightarrow\) \(N\)-dimensional Taylor expansion up to the first order!
  \(\Rightarrow\) Thus, total derivative is the generalization of the direction to the case \(N,M\).

• \[\vec{A} \cdot \vec{h}=\vec0\]

  is the parametrization of an \(M\) dimensional hyperplane at the point \(\vec{h}=\vec0\), i.e. at \(\vec{x}\) that ”touches” the \(M\)-D-function

• Note: \(\vec{f}:\mathbb{R}^N\to\mathbb{R}^M\). If total derivative exists then
  \(\rightarrow\) all partial derivatives \(\frac{\partial f_k}{\partial x_j}\) of all components with respect to all variables are well defined!

\begin{eqnarray*}\mbox{total derivative}&\Rightarrow&\mbox{partial derivatives}\\ &\not\Leftarrow&\mbox{not in general, but for all ''friendly'' functions o.k. }\\ \mbox{Hence: total}&\Leftrightarrow&\mbox{partial} \end{eqnarray*}

Examples

1. \(f:\mathbb{R}^N\to\mathbb{R}\) \begin{eqnarray*}f(\vec{x})&=&\left(x_1,\ldots,x_N\right)^\top\cdot\tilde{c}\vect{x_1\\\vdots\\x_N}\quad\mbox{$\tilde c-N\times N$ Matrix symmetric!}\\ \mbox{total derivative:}\\ f(\vec{x}+\vec{h})-f(\vec{x})&=&(\vec{x}+\vec{h})\cdot\tilde c(\vec{x}+\vec{h})-\vec{x}\cdot\tilde{c}\vec{x}\\ &=&(\vec{x}+\vec{h})\cdot(\tilde c\vec{x}+\tilde c\vec{h})-\vec{x}\cdot\tilde{c}\vec{x}\\ &=&\vec{x}\tilde c\vec{x}+\vec{h}\tilde c\vec{x}+\vec{x}\tilde c\vec{h}+\vec{h}\tilde c\vec{h}-\vec{x}\cdot\tilde{c}\vec{x}\\ &=&\vec h\tilde c\vec x+\vec x\tilde c\vec h+\vec h\tilde c\vec h\\ &=&(\tilde c\vec x)\cdot\vec{h}+(\tilde c\vec x)\cdot\vec h+(\tilde c\vec h)\cdot\vec h=2(\tilde c\vec x)\vec h+\underbrace{(\tilde c\vec h)\cdot\vec h}_{\varphi(\vec h)}\\ \Rightarrow:&&\mbox{total derivative:}\;\;f'(\vec{x})=2\tilde c\vec x=\vec\nabla f \end{eqnarray*}

2. \(\vec{f}:\mathbb{R}^2\to\mathbb{R}^2\) \begin{eqnarray*} \vec f(x_1,x_2)&=&\vect{x_1+x_2^2\\x_1^2}\qquad\quad\vec h=\vect{h_1\\h_2}\\ \vec f(\vec x+\vec h)-\vec f(\vec x)&=&\vect{x_1+h_1+(x_2+h_2)^2\\(x_1+h_1)^2}-\vect{x_1+x_2^2\\x_1^2}\\ &=&\vect{h_1+2x_2h_2+h_2^2\\2x_1h_1+h_1^2}=\tilde A\vec h+\tilde\varphi(\vec h)\\ &=&\vect{h_1+2x_2h_2\\2x_1h_1+0\cdot h_2}+\vect{h_2^2\\h_1^2}=\left(\begin{array}{cc} 1 & 2 x_2 \\ 2 x_1 & 0 \end{array} \right)\vect{h_1\\h_2}+\vect{h_2^2\\h_1^2}\\ \frac{\vect{h_2^2\\h_1^2}}{|\vec h|}&=&\vect{\frac{h_2^2}{\sqrt{h_1^2+h_2^2}}\\\frac{h_1^2}{\sqrt{h_1^2+h_2^2}}}\begin{array}{lclcc} 0\lt\frac{h_2^2}{\sqrt{h_1^2+h_2^2}}\lt\frac{h_2^2}{h_2}&=&h_2&\to&0\\0\lt\frac{h_1^2}{\sqrt{h_1^2+h_2^2}}\lt\frac{h_1^2}{h_1}&=&h_1&\to&0\end{array}\;\frac{\tilde\varphi(\vec h)}{|\vec h|}\to 0 \end{eqnarray*}

In general:

than: total derivative is given by the Matrix:

\(M=1:\;\tilde A=\left(\frac{\partial f_1}{\partial x_1}\cdots\frac{\partial f_1}{\partial x_N}\right)^\top\)
\(\tilde A\) is called Jacobi-Matrix of \(\vec f\) or the differential of \(\vec f\) and \(\det \tilde A\) is called the Jacobi or Functional determinant of \(\vec f\).

© J. Carstensen (Math for MS)